题目内容
13.若以x轴正方向为始边,曲线上的点与圆心的连线为终边的角θ为参数,则圆x2+y2-2x=0的参数方程为$\left\{\begin{array}{l}{x=cosθ+1}\\{y=sinθ}\end{array}\right.$(θ为参数).分析 求出圆的圆心和半径,在圆上任取点P(x,y),用θ表示出P点的横纵坐标即可.
解答  解圆x2+y2-2x=0的标准方程为(x-1)2+y2=1.故圆心坐标为(1,0),半径为1.
解圆x2+y2-2x=0的标准方程为(x-1)2+y2=1.故圆心坐标为(1,0),半径为1.
在圆上任取一点P(x,y),则x-1=cosθ,y=sinθ.
∴x=cosθ+1,y=sinθ.
∴圆的参数方程为$\left\{\begin{array}{l}{x=cosθ+1}\\{y=sinθ}\end{array}\right.$(θ为参数).
故答案为$\left\{\begin{array}{l}{x=cosθ+1}\\{y=sinθ}\end{array}\right.$(θ为参数).
点评 本题考查了圆的参数方程,参数的几何意义,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
3.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{3}$=1(a>0)过点(-2,0),则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
4.已知抛物线x2=2py的准线方程为y=-$\frac{1}{4}$,函数f(x)=sinωx的周期为4,则抛物线与函数f(x)在第一象限所围成的封闭图形的面积为( )
| A. | $\frac{6-π}{3π}$ | B. | 1 | C. | $\frac{π}{2}$ | D. | $\frac{4-π}{2π}$ |
8.在正方体ABCD-A1B1C1D1中,P是A1D上的一点,且满足A1P=2PD,下列命题正确的是( )
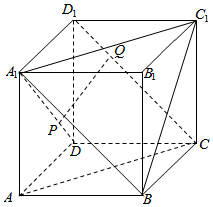

| A. | 在CD1上存在点Q,使得PQ∥平面AA1C1C | |
| B. | 在CD1上存在点Q,使得PQ⊥平面AA1C1C | |
| C. | 在CD1上存在点Q,使得PQ∥平面A1BC1 | |
| D. | 在CD1上存在点Q,使得PQ⊥平面A1BC1 |