题目内容
如图,底面 是边长为2的菱形,且
是边长为2的菱形,且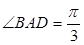 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥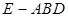 与
与 ,且
,且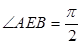 .
.
(1)求证: 平面
平面 ;
;
(2)求多面体 的体积.
的体积.
(1)证明过程见解析;(2) .
.
解析试题分析:(1)作 面
面 于
于 ,作
,作 面
面 于
于 ,易判断四边形
,易判断四边形 是平行四边形,从而有
是平行四边形,从而有 ,又
,又 面
面
 面
面 ,所以
,所以 平面
平面 ;
;
(2)取 的中点
的中点 ,连接
,连接 ,
, ,则多面体
,则多面体 分割成
分割成 ,
, ,
, ,分别求出此三个三棱锥的体积,即可求出多面体
,分别求出此三个三棱锥的体积,即可求出多面体 的体积.
的体积.
(1)作 面
面 于
于 ,作
,作 面
面 于
于 ,
,
因 与
与 都是正三棱锥,
都是正三棱锥,
且 、
、 分别为
分别为 与
与 的中心,
的中心, 且
且 .
.
所以四边形 是平行四边形,所以
是平行四边形,所以 .
.
又 面
面
 面
面 ,所以
,所以 平面
平面 .
.
(2)又 ,则
,则 平面
平面 , 故
, 故 .
.
取 中点为
中点为 ,联接
,联接 ,即
,即 平面
平面 ,
,
易算出

故多面体 的体积
的体积

考点:线面平行的判定;空间几何体的体积.

练习册系列答案
相关题目
 为圆
为圆 的直径,
的直径, 为圆周上异于
为圆周上异于 、
、 的一点,
的一点, 垂直于圆
垂直于圆 于
于 ,
, 于点
于点 .
. 平面
平面 ;
; ,
, ,求四面体
,求四面体 的体积.
的体积.
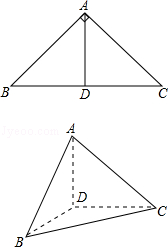

 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积. 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点,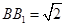 ,
,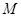 是线段
是线段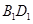 的中点.
的中点.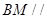 平面
平面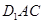 ;
;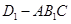 的体积.
的体积.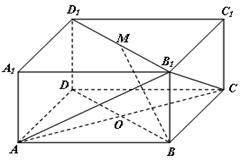
 中,
中, ,
, ,
, ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、 ,与
,与 ),将△
),将△
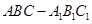 中,
中,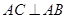 ,
, 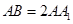 ,
,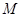 是
是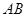 的中点,△
的中点,△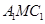 是等腰三角形,
是等腰三角形,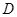 为
为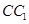 的中点,
的中点,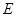 为
为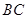 上一点.
上一点.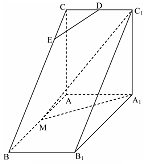
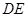 ∥平面
∥平面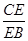 ;
;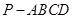 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面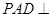 底面
底面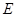 为
为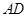 的中点,
的中点, 是棱
是棱 的中点,
的中点,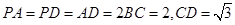 .
.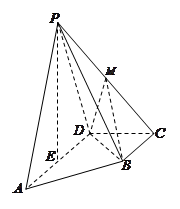
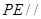 平面
平面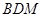 ;
;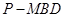 的体积.
的体积. 所在的平面和平面
所在的平面和平面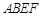 互相垂直,等腰梯形
互相垂直,等腰梯形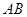 ∥
∥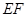 ,
,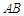 =2,
=2,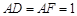 ,
,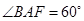 ,
, ,
, 分别为
分别为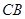 的中点,
的中点,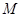 为底面
为底面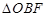 的重心.
的重心.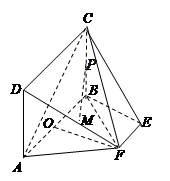
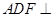 平面
平面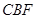 ;
;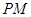 ∥平面
∥平面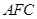 ;
; 的体积
的体积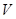 .
.