题目内容
如图甲,在平面四边形ABCD中,已知
 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
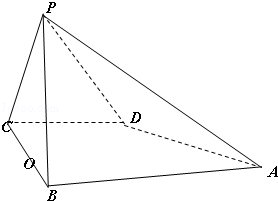
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
平面BDC(如图乙),设点E,F分别为棱AC,AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
(1)证明:见解析;(2)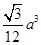 .
.
解析试题分析:(1)注意分析折叠前后变化的关系及不变化的关系.在图甲中可得 ;
;
在图乙中,可得AB⊥CD.根据DC⊥BC,即可得到DC⊥平面ABC.
(2)首先根据E,F分别为AC,AD的中点,得到EF//CD,根据(1)知,DC⊥平面ABC,得到EF⊥平面ABC,从而得到
在图甲中,根据给定角度及长度,计算“不变量”,得,BD=2 ,BC=
,BC=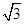
 ,EF=
,EF= CD=
CD=
 ,
,
利用体积公式计算即得所求.
解答本题的关键是确定“垂直关系”,这也是难点所在,平时学习中,应特别注意转化意识的培养,等体积转化的方法,是立体几何中常用方法之一.
(1)证明:在图甲中∵ 且
且 ∴
∴ ,
,
即 1分
1分
在图乙中,∵平面ABD⊥平面BDC , 且平面ABD∩平面BDC=BD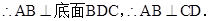 4分
4分
又 ,
,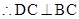 ,且
,且 ,∴DC⊥平面ABC. 6分
,∴DC⊥平面ABC. 6分
(2)解: , 7分
, 7分
又由(1)知,DC⊥平面ABC,∴EF⊥平面ABC, 8分
所以, 9分
9分
在图甲中, 
由 得,
得, ,
, 10分
10分 ,
, 11分
11分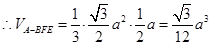 12分
12分
考点:平行关系,垂直关系,几何体的体积.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目

 (d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.
(d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.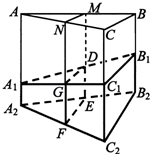
 是边长为2的菱形,且
是边长为2的菱形,且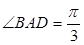 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥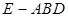 与
与 ,且
,且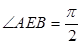 .
.
 平面
平面 的体积.
的体积. 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
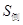 的值;
的值; 是半圆弧
是半圆弧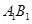 的中点,点
的中点,点 在半径
在半径 上,且
上,且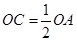 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.
 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若 ,
, ,则此球的表面积等于 。
,则此球的表面积等于 。 ,则原四边形的面积是多少?
,则原四边形的面积是多少?