题目内容
如图,△ 中,
中, ,
, ,
, ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边 上,半圆与
上,半圆与 、
、 分别相切于点
分别相切于点 、
、 ,与
,与 交于点
交于点 ),将△
),将△ 绕直线
绕直线 旋转一周得到一个旋转体.
旋转一周得到一个旋转体.
(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.
(1) ;(2)
;(2) .
.
解析试题分析:(1)要求球的表面积,首先要求出球的半径,如图即半圆 的半径,这可在
的半径,这可在 中列方程解得,圆
中列方程解得,圆 半径为
半径为 则有
则有 ,即
,即 ,则此求得
,则此求得 ;(3)要阴影部分旋转后的体积,我们要看阴影部分是什么几何体,看看能不能把变成我们熟知的锥台、球,或者上它们构成的,本题中,是在三角形内部挖去一个小三角形,因此最后所得可以看作是一个圆锥里面挖去了一个球,从而其体积就等于一个圆锥的体积减去球的体积,即
;(3)要阴影部分旋转后的体积,我们要看阴影部分是什么几何体,看看能不能把变成我们熟知的锥台、球,或者上它们构成的,本题中,是在三角形内部挖去一个小三角形,因此最后所得可以看作是一个圆锥里面挖去了一个球,从而其体积就等于一个圆锥的体积减去球的体积,即 .
.
试题解析:(1)连接 ,则
,则 ,
,
设 ,则
,则 ,
,
在 中,
中, ,
,
所以 (4分)
(4分)
所以 . (6分)
. (6分)
(2)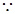
 中,
中, ,
, ,
, ,
, , (8分)
, (8分) .(12分)
.(12分)
考点:球的表面积;(2)旋转体的体积.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,点M在线段EC上且不与E、C垂合.
,点M在线段EC上且不与E、C垂合. 时,求三棱锥M—BDE的体积
时,求三棱锥M—BDE的体积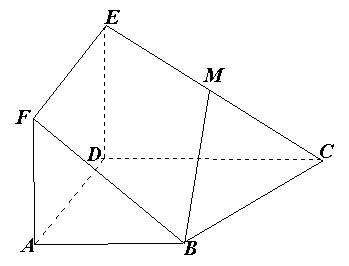
 (d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.
(d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.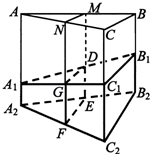
 是边长为2的菱形,且
是边长为2的菱形,且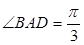 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥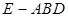 与
与 ,且
,且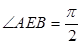 .
.
 平面
平面 的体积.
的体积. AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.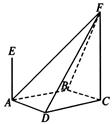
 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
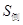 的值;
的值; 是半圆弧
是半圆弧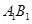 的中点,点
的中点,点 在半径
在半径 上,且
上,且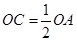 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.
 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积.