题目内容
如图所示的长方体 中,底面
中,底面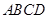 是边长为
是边长为 的正方形,
的正方形,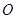 为
为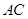 与
与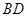 的交点,
的交点,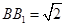 ,
,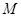 是线段
是线段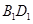 的中点.
的中点.
(1)求证: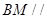 平面
平面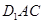 ;
;
(2)求三棱锥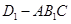 的体积.
的体积.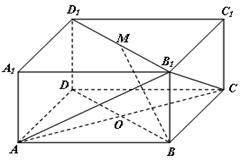
(1)证明过程详见试题解析;(2)三棱锥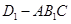 的体积为
的体积为 .
.
解析试题分析:(1)连接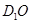 ,要证
,要证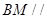 平面
平面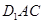 ,需证
,需证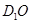 ∥
∥ ,而
,而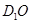 ∥
∥ 易证;
易证;
(2)用割补法,用长方体的体积减去四个三棱锥的体积即可,求得结果为 .
.
试题解析:(1) 连结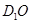 ,如图,
,如图,
∵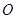 、
、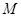 分别是
分别是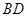 、
、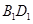 的中点,
的中点, 是矩形,
是矩形,
∴四边形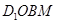 是平行四边形,
是平行四边形,
∴ . 2分
. 2分
∵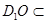 平面
平面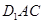 ,
, 平面
平面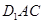 ,
,
∴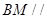 平面
平面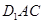 . 6分
. 6分
(2) 解法1 连结 ,∵正方形
,∵正方形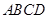 的边长为2,
的边长为2,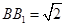 ,∴
,∴ ,
, ,
,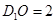 ,则
,则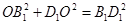 ,
,
∴ . 8分
. 8分
又∵在长方体 中,
中, ,
, ,且
,且 ,
,
∴ 平面
平面 ,又
,又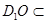 平面
平面 ,
,
∴ ,又
,又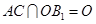 ,
,
∴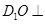 平面
平面 ,即
,即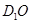 为三棱锥
为三棱锥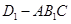 的高. 10分
的高. 10分
∵ ,
,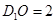
∴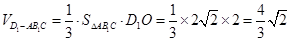 . 12分
. 12分
解法2: 三棱锥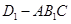 是长方体
是长方体 割去三棱锥
割去三棱锥 、三棱锥
、三棱锥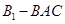 、三棱锥
、三棱锥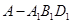 、三棱锥
、三棱锥 后所得,而三棱锥
后所得,而三棱锥 、
、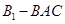 、
、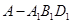 、
、 是等底等高,故其体积相等.
是等底等高,故其体积相等.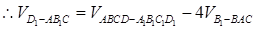
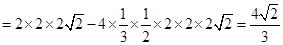 .
.
考点:线面平行的判定定理、空间几何体的表面积和体积.

练习册系列答案
相关题目


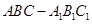 中,平面
中,平面 平面ABC,
平面ABC, ,
,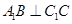 ,
,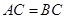 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.


 是边长为2的菱形,且
是边长为2的菱形,且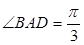 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥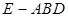 与
与 ,且
,且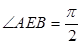 .
.
 平面
平面 的体积.
的体积. ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
 ,求证:
,求证: ;
;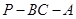 的大小为
的大小为 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥 的体积为
的体积为 .
.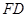 垂直于矩形
垂直于矩形 所在平面,
所在平面,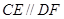 ,
, .
.
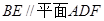 ;
; 的一个边
的一个边 ,
, ,则另一边
,则另一边 的长为何值时,三棱锥
的长为何值时,三棱锥 的体积为
的体积为 ?
? A1B1C1中,D,E分别是AB,BB1的中点.
A1B1C1中,D,E分别是AB,BB1的中点.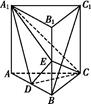
 ,求三棱锥C
,求三棱锥C