题目内容
7.已知实数p>0,直线4x+3y-2p=0与抛物线y2=2px和圆(x-$\frac{p}{2}$)2+y2=$\frac{{p}^{2}}{4}$从上到下的交点依次为A,B,C,D,则$\frac{|AC|}{|BD|}$的值为( )| A. | $\frac{1}{8}$ | B. | $\frac{5}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{7}{16}$ |
分析 设A(x1,y1),D(x2,y2),抛物线的焦点为F,由题得|BF|=|CF|=$\frac{p}{2}$.由抛物线的定义得:|AC|=|AF|+|CF|=$\frac{p}{2}$+x1+$\frac{p}{2}$=x1+p,同理得|BD|=x2+p.联立直线4x+3y-2p=0与抛物线y2=2px且消去x解出y1=$\frac{p}{2}$,y2=-2p,所以x1=$\frac{p}{8}$,x2=2p,进而得到答案.
解答 解:设A(x1,y1),D(x2,y2),抛物线的焦点为F,
由题意得|BF|=|CF|=$\frac{p}{2}$
由抛物线的定义得:|AC|=|AF|+|CF|=$\frac{p}{2}$+x1+$\frac{p}{2}$=x1+p,同理得|BD|=x2+p.
联立直线4x+3y-2p=0与抛物线y2=2px且消去x得:2y2+3py-2p2=0
解得:y1=$\frac{p}{2}$,y2=-2p,所以x1=$\frac{p}{8}$,x2=2p
所以$\frac{|AC|}{|BD|}$=$\frac{\frac{9}{8}p}{3p}$=$\frac{3}{8}$.
故选:C.
点评 解决此类题目的关键是对抛物线的定义要熟悉,即抛物线上的点到定点的距离与到定直线的距离相等.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.若将函数y=3sin(6x+$\frac{π}{6}$)的图象上各点的横坐标伸长到原来的3倍(纵坐标不变),再向右平移$\frac{π}{6}$个单位长度,得到函数y=f(x)的图象,若y=f(x)+a在x∈[-$\frac{π}{6}$,$\frac{π}{2}$]上有两个不同的零点,则实数a的取值范围是( )
| A. | [-3,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,3] | D. | (-3,-$\frac{3}{2}$] |
12.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 12 | D. | $\sqrt{10}$ |
19.已知f(x)=$\left\{\begin{array}{l}{x+3,x≤1}\\{-{x}^{2}+2x+3,x>1}\end{array}\right.$,则使得f(x)-ex-m≤0恒成立的m的取值范围是( )
| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘成频率分布直方图(如图).
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘成频率分布直方图(如图).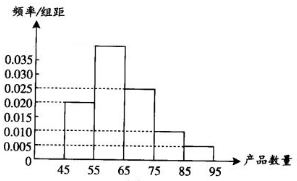 为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为0.4;这20名工人中一天生产该产品数量在[55,75)的人数是13.
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为0.4;这20名工人中一天生产该产品数量在[55,75)的人数是13.