题目内容
设三角形ABC的内角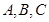 所对的边长分别为
所对的边长分别为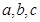 ,
,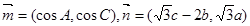 ,且
,且 .
.
(Ⅰ)求角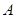 的大小;
的大小;
(Ⅱ)若AC=BC,且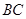 边上的中线
边上的中线 的长为
的长为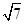 ,求
,求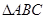 的面积.
的面积.
(Ⅰ)A= ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)由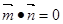 可得
可得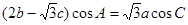 通过三角运算即sin(A+C)=sinB.可求得角A的值.
通过三角运算即sin(A+C)=sinB.可求得角A的值.
(Ⅱ)由角A= .可求得C=
.可求得C=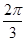 .又因为AC=2CM.即AM=
.又因为AC=2CM.即AM= 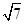 .在三角形AMC中可求得AC的长.再用三角形面积公式即可求得三角形的面积.本题是利用向量垂直知识来求得角A.再根据等腰三角形的内角关系,利用余弦定理求得三角形的面积.
.在三角形AMC中可求得AC的长.再用三角形面积公式即可求得三角形的面积.本题是利用向量垂直知识来求得角A.再根据等腰三角形的内角关系,利用余弦定理求得三角形的面积.
试题解析:(1)由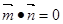
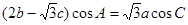 1分
1分
所以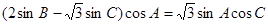 2分
2分
则2sinBcosA=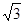 sinB 4分
sinB 4分
所以cosA=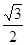 于是A=
于是A= 6分
6分
(2)由(1)知A= ,又AC=BC,所以C=
,又AC=BC,所以C=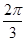 7分
7分
设AC=x,则MC=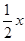 ,AM=
,AM=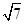 ,在
,在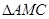 中,由余弦定理得
中,由余弦定理得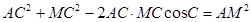 9分
9分
即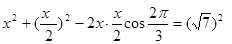
解得x=2 11分
故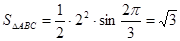 13分
13分
考点:1.向量的垂直坐标形式的表示.2.余弦定理.3.三角恒等变换.

练习册系列答案
相关题目
 中,角A,B,C所对边分别为a,b,c,且向量
中,角A,B,C所对边分别为a,b,c,且向量 ,
, ,满足
,满足
 成等差数列,且
成等差数列,且 ,求边
,求边 的长
的长 中,
中, 、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,角C是锐角,且
所对的边,角C是锐角,且 。
。 ,
,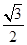 ,求
,求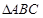 的内角A、B、C所对的边为
的内角A、B、C所对的边为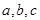 ,
,  ,
, 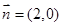 ,且
,且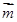 与
与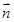 所成角为
所成角为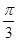 .
. 的取值范围.
的取值范围. .
. 的最小值和最小正周期;
的最小值和最小正周期; 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值.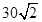 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于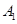 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西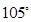 方向的
方向的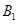 处,此时两船相距
处,此时两船相距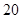 海里,当甲船航行
海里,当甲船航行 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的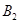 处,此时两船相距
处,此时两船相距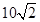 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?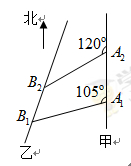
 ABC中,内角A,B,C的对边分别为a,b,c.
ABC中,内角A,B,C的对边分别为a,b,c. ,
, .
. 的值; (Ⅱ)若
的值; (Ⅱ)若 ,求
,求 的内角
的内角 所对边的长分别为
所对边的长分别为 ,且有
,且有 .
.
 ,
, ,
, 为
为 的中点,求
的中点,求 的长.
的长.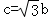 .
.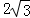 ,求a,b的值.
,求a,b的值.