题目内容
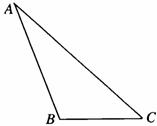
(17)如图,在△ABC中,AC=2,BC=1,cosC=(Ⅰ)求AB的值;
(Ⅱ)求sin(
本小题考查同角三角函数关系、两角和公式、倍角公式、正弦定理、余弦定理等基础知识,考查基本运算能力及分析和解决问题的能力.
(Ⅰ)解:由余弦定理,
AB2=AC2+BC2
=4+1-2×2×1×![]() =2.
=2.
那么,AB=![]() .
.

(Ⅱ)解:由cosC=![]() 且0<C<π,得sinC=
且0<C<π,得sinC=![]() 由正弦定理,
由正弦定理,
![]() ,
,
解得sinA=![]() ,所以,cosA=
,所以,cosA=![]() .由倍角公式
.由倍角公式
sin![]() ,
,
且cos![]() ,故
,故
sin(![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )| A、5.16 | B、6.16 | C、18.84 | D、17.84 |
 4、某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:每一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可以分析出x和y分别为( )
4、某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:每一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可以分析出x和y分别为( ) 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,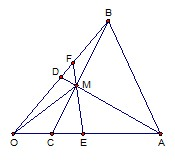 如图,在△ABO中,
如图,在△ABO中,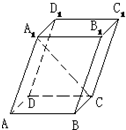 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )