题目内容
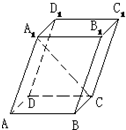 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )A、
| ||
B、2
| ||
C、
| ||
D、
|
分析:点A1在底面的投影O在底面正方形对角线AC上,过A1作A1E⊥AB于E,求出AE,连结OE,则OE⊥AB,∠EAO=45°,在Rt△AEO,求出OC,然后求解A1O,即可求解A1C.
解答:解:由已知可得点A1在底面的投影O在底面正方形对角线AC上,
过A1作A1E⊥AB于E,
在Rt△AEA1,AA1=3,∠A1AE=60°
∴AE=
,连结OE,则OE⊥AB,∠EAO=45°,
在Rt△AEO中,AO=
,又AC=2
∴OC=
,
在Rt△AOA1,AA1=3,AO=
,∴A1O=
,
在Rt△A1OC,A1C=
=
故选A.
过A1作A1E⊥AB于E,
在Rt△AEA1,AA1=3,∠A1AE=60°
∴AE=
| 3 |
| 2 |
在Rt△AEO中,AO=
3
| ||
| 2 |
| 2 |
| ||
| 2 |
在Rt△AOA1,AA1=3,AO=
3
| ||
| 2 |
3
| ||
| 2 |
在Rt△A1OC,A1C=
| A1O2+OC2 |
| 5 |
故选A.
点评:本题考查几何法求解空间两点的距离,也可以利用空间向量的模求解距离,考查计算能力与逻辑推理能力.

练习册系列答案
相关题目
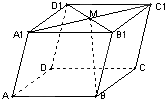 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
 如图,在平行六面体ABCD-A1B1C1D1中,已知
如图,在平行六面体ABCD-A1B1C1D1中,已知| AB |
| AD |
| AA1 |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
 如图,在平行六面体ABCD-A1B1C1D1中,若
如图,在平行六面体ABCD-A1B1C1D1中,若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| D1B |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
 对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则
对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则 (2001•上海)如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若
(2001•上海)如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若