题目内容
(本小题满分14分)(注意:仙中、一中、八中的学生三问全做,其他学校的学生只做前两问)
已知函数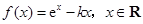
(Ⅰ)若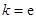 ,试确定函数
,试确定函数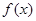 的单调区间;
的单调区间;
(Ⅱ)若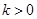 ,且对于任意
,且对于任意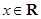 ,
,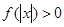 恒成立,试确定实数
恒成立,试确定实数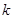 的取值范围;
的取值范围;
(Ⅲ)设函数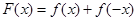 ,求证:
,求证: .
.
已知函数
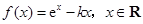
(Ⅰ)若
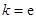 ,试确定函数
,试确定函数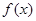 的单调区间;
的单调区间;(Ⅱ)若
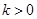 ,且对于任意
,且对于任意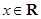 ,
,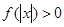 恒成立,试确定实数
恒成立,试确定实数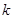 的取值范围;
的取值范围;(Ⅲ)设函数
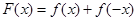 ,求证:
,求证: .
. (Ⅰ) 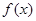 的单调递增区间是
的单调递增区间是 ,
,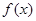 的单调递减区间是
的单调递减区间是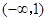 .
.
(Ⅱ)实数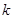 的取值范围是
的取值范围是 .(Ⅲ)见解析。
.(Ⅲ)见解析。
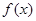 的单调递增区间是
的单调递增区间是 ,
,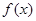 的单调递减区间是
的单调递减区间是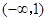 .
. (Ⅱ)实数
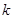 的取值范围是
的取值范围是 .(Ⅲ)见解析。
.(Ⅲ)见解析。本试题主要是考查了导数在研究函数中的运用。
(1)因为由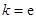 得
得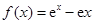 ,所以
,所以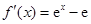 .然后根据导数的符号判定单调性得到及结论
.然后根据导数的符号判定单调性得到及结论
(2)由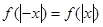 可知
可知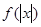 是偶函数.
是偶函数.
于是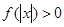 对任意
对任意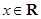 成立等价于
成立等价于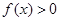 对任意
对任意 成立.然后求解导数,分析得到参数的范围。
成立.然后求解导数,分析得到参数的范围。
(3)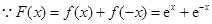 ,
,
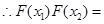
 ,
,
运用放缩法得到结论。
解:(Ⅰ)由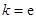 得
得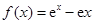 ,所以
,所以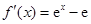 .
.
由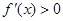 得
得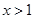 ,故
,故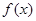 的单调递增区间是
的单调递增区间是 ,
,
由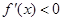 得
得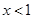 ,故
,故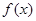 的单调递减区间是
的单调递减区间是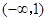 .(6分)(3分)
.(6分)(3分)
(Ⅱ)由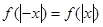 可知
可知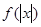 是偶函数.
是偶函数.
于是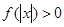 对任意
对任意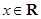 成立等价于
成立等价于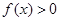 对任意
对任意 成立.(8分)(5分)
成立.(8分)(5分)
由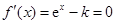 得
得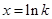 .
.
①当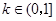 时,
时,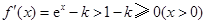 .此时
.此时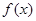 在
在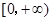 上单调递增.
上单调递增.
故 ,符合题意. (10分)(7分)
,符合题意. (10分)(7分)
②当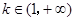 时,
时,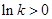 .当
.当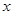 变化时
变化时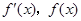 的变化情况如下表:
的变化情况如下表:
由此可得,在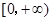 上,
上,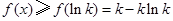 .
.
依题意,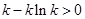 ,又
,又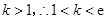 .(13分)(9分)
.(13分)(9分)
综合①,②得,实数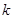 的取值范围是
的取值范围是 .(14分)(10分)
.(14分)(10分)
(Ⅲ)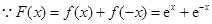 ,
,
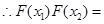
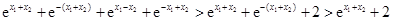 ,
,
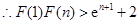 ,
,
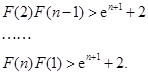
由此得,
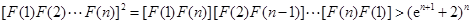
故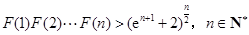 .((14分)
.((14分)
(1)因为由
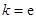 得
得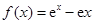 ,所以
,所以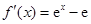 .然后根据导数的符号判定单调性得到及结论
.然后根据导数的符号判定单调性得到及结论(2)由
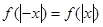 可知
可知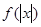 是偶函数.
是偶函数.于是
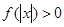 对任意
对任意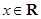 成立等价于
成立等价于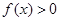 对任意
对任意 成立.然后求解导数,分析得到参数的范围。
成立.然后求解导数,分析得到参数的范围。(3)
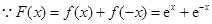 ,
,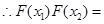
 ,
,运用放缩法得到结论。
解:(Ⅰ)由
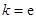 得
得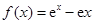 ,所以
,所以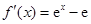 .
.由
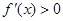 得
得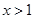 ,故
,故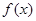 的单调递增区间是
的单调递增区间是 ,
,由
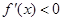 得
得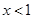 ,故
,故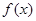 的单调递减区间是
的单调递减区间是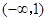 .(6分)(3分)
.(6分)(3分)(Ⅱ)由
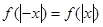 可知
可知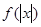 是偶函数.
是偶函数.于是
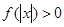 对任意
对任意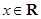 成立等价于
成立等价于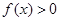 对任意
对任意 成立.(8分)(5分)
成立.(8分)(5分)由
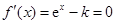 得
得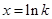 .
.①当
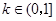 时,
时,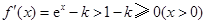 .此时
.此时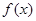 在
在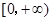 上单调递增.
上单调递增.故
 ,符合题意. (10分)(7分)
,符合题意. (10分)(7分)②当
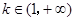 时,
时,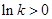 .当
.当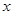 变化时
变化时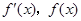 的变化情况如下表:
的变化情况如下表: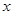 | 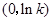 | 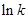 | 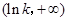 |
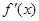 | 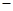 |  |  |
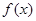 | 单调递减 | 极小值 | 单调递增 |
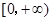 上,
上,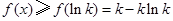 .
.依题意,
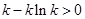 ,又
,又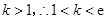 .(13分)(9分)
.(13分)(9分)综合①,②得,实数
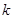 的取值范围是
的取值范围是 .(14分)(10分)
.(14分)(10分)(Ⅲ)
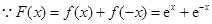 ,
,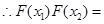
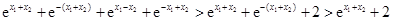 ,
,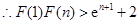 ,
,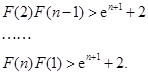
由此得,
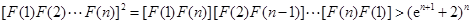
故
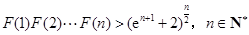 .((14分)
.((14分)
练习册系列答案
相关题目
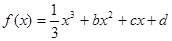 ,设曲线
,设曲线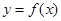 在与
在与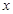 轴交点处的切线为
轴交点处的切线为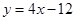 ,
,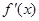 为
为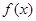 的导函数,满足
的导函数,满足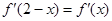 .
.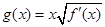 ,
,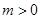 ,求函数
,求函数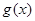 在
在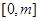 上的最大值;
上的最大值;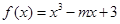 ,若
,若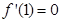 ,则
,则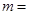 .
.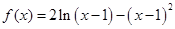 .
.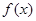 的单调递增区间;
的单调递增区间;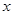 的方程
的方程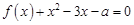 在区间
在区间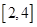 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数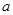 的取值范围.
的取值范围. 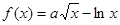
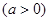
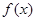 在
在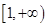 上递增,求
上递增,求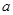 的取值范围;
的取值范围;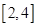 上的存在单调递减区间 ,求
上的存在单调递减区间 ,求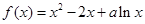 。
。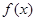 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数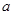 的取值范围;
的取值范围; 的导函数是
的导函数是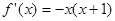 ,则函数
,则函数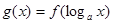
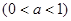

 ,
,

 ,
,
 的单调递减区间是
的单调递减区间是


