Question

11．O是坐标原点，点A（-1，1），点P（x，y）为平面区域$\left\{\begin{array}{l}{x≥0}\\{2x-y≤0}\\{y≤kx+1}\end{array}\right.$的一个动点，函数f（λ）=|$\overrightarrow{OP}$-λ$\overrightarrow{OA}$|（λ∈R）的最小值为M，若M≤$\frac{3}{2}$$\sqrt{2}$恒成立，则k的取值范围是（　　）

• A． k≤1
• B． -1≤k≤1
• C． 0≤k≤3
• D． k≤1或≥3

Answer 1

分析 画出满足条件的可行域，分析出函数f（λ）的最小值为M≤$\frac{3}{2}$$\sqrt{2}$恒成立表示可行域内的点到直线OA：x+y=0的最大距离不大于$\frac{3}{2}$$\sqrt{2}$，结合可行域的图象，分类讨论，可得答案．

解答 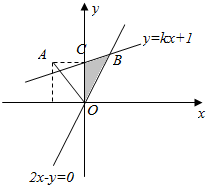解：满足约束条件$\left\{\begin{array}{l}x≥0\\ 2x-y≤0\\ y≤kx+1\end{array}\right.$的可行域如下图所示：

函数f（λ）=|$\overrightarrow{OP}$-λ$\overrightarrow{OA}$|（λ∈R）表示P点到直线OA上一点的距离，
若函数f（λ）的最小值为M≤$\frac{3}{2}$$\sqrt{2}$恒成立，
则仅需可行域内的点到直线OA：x+y=0的最大距离不大于$\frac{3}{2}$$\sqrt{2}$即可，
若k≥2，则不存在满足条件的点，
若k＜2，则存在B点（$\frac{1}{2-k}$，$\frac{2}{2-k}$）到直线OA：x+y=0的距离最远，
此时d=$\frac{\left|\frac{3}{2-k}\right|}{\sqrt{2}}$≤$\frac{3}{2}$$\sqrt{2}$，
解得：k≤1，
故选：A

点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法及分类讨论的数学思想方法，关键是对题意的理解，是难题．