题目内容
已知长方体的全面积为8cm2,则它的对角线长的最小值为 cm.
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:设长、宽、高分别是a,b,c,则全面积可表示为:2a•b+2b•c+2c•a=8,即ab+bc+ac=4,利用对角线长为
≥
,即可得出结论.
| a2+b2+c2 |
| ab+bc+ac |
解答:
解:设长、宽、高分别是a,b,c,则全面积可表示为:2a•b+2b•c+2c•a=8,即ab+bc+ac=4
对角线长为
≥
,当且仅当a=b=c时,有最小值为2.
故答案为:2.
对角线长为
| a2+b2+c2 |
| ab+bc+ac |
故答案为:2.
点评:本题考查基本不等式在最值问题中的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知点A(-1,2),B(2,7),在x轴上有一点P,使得|PA|+|PB|最小的值为$( )
A、3
| ||
B、
| ||
C、2
| ||
| D、9 |
以原点为中心,对角线在坐标轴上,边长为1的正方形的四条边的方程为( )
A、|x|+|y|=
| ||||
| B、|x|+|y|=1 | ||||
C、|x+y|=
| ||||
| D、|x+y|=1 |
已知f(x)=(x-m)(x-n)=(x-a)(x-b)+1,若m>n且a>b,则a,b,m,n的大小顺序是( )
| A、m>n>a>b |
| B、a>m>n>b |
| C、m>a>b>n |
| D、a>b>m>n |

 将 3 种农作物都种植在如图的 4 块试验田里,每块种植一种农作物,要求相邻的试验田不能种植同一种作物,则不同的种植方法共有( )种.
将 3 种农作物都种植在如图的 4 块试验田里,每块种植一种农作物,要求相邻的试验田不能种植同一种作物,则不同的种植方法共有( )种.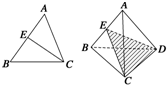 在平面几何中,△ABC的内角平分线CE分AB所成线段的比
在平面几何中,△ABC的内角平分线CE分AB所成线段的比