题目内容
在△ 中,
中, 是角
是角 对应的边,向量
对应的边,向量 ,
, ,且
,且 .
.
(1)求角 ;
;
(2)函数 的相邻两个极值的横坐标分别为
的相邻两个极值的横坐标分别为 、
、 ,求
,求 的单调递减区间.
的单调递减区间.
(1)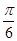 ;(2)
;(2)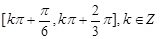 .
.
解析试题分析:本题主要考查向量的数量积、余弦定理、诱导公式、降幂公式、两家和与差的正弦公式、三角函数图像、三角函数的性质等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力和数形结合思想.第一问,利用向量的数量积转化表达式,由于得到的表达式的形式类似于余弦定理,所以利用余弦定理求角C;第二问,利用三角形的内角和为 ,转化
,转化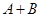 为
为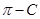 ,将C角代入再利用倍角公式、降幂公式、两角和的正弦公式化简表达式为
,将C角代入再利用倍角公式、降幂公式、两角和的正弦公式化简表达式为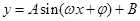 的形式,数形结合得到三角函数的周期,确定解析式后,再数形结合求函数的单调减区间.
的形式,数形结合得到三角函数的周期,确定解析式后,再数形结合求函数的单调减区间.
(1)因为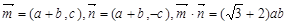 ,所以
,所以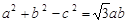 ,
,
故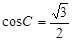 ,
,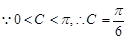 . 5分
. 5分
(2)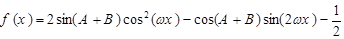
=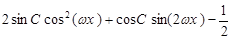
=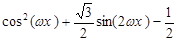
=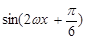 8分
8分
因为相邻两个极值的横坐标分别为 、
、 ,所以
,所以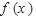 的最小正周期为
的最小正周期为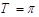 ,
,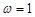
所以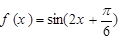 10分
10分
由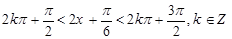
所以 的单调递减区间为
的单调递减区间为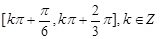 . 12分
. 12分
考点:向量的数量积、余弦定理、诱导公式、降幂公式、两家和与差的正弦公式、三角函数图像、三角函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的三内角
的三内角 、
、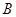 、
、 所对的边分别是
所对的边分别是 ,
, ,
, ,向量
,向量
 ,且
,且 。
。 ,求
,求 的范围。
的范围。
 北偏东
北偏东 方向的
方向的 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得 距离为31
距离为31 ,该小汽车从
,该小汽车从 处,测得离电视塔21
处,测得离电视塔21 、
、 、
、 、
、 ,欲测量
,欲测量 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
, ,
,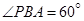 ,
, ,则
,则
 中,
中, 分别是
分别是 所对的边,
所对的边, ,
, ,三角形的面积为
,三角形的面积为 ,
, 的大小; (2)求
的大小; (2)求 的值.
的值.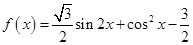 .
.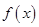 的最小正周期及在区间
的最小正周期及在区间 的最大值;
的最大值; 中,
中, 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,
, ,
, ,求
,求 周长
周长 的最大值.
的最大值. 中,角
中,角 所对的边分别为
所对的边分别为 ,点
,点 在直线
在直线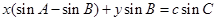 上.
上.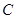 的值;
的值; ,且
,且 ,求
,求 .
. 中,
中,
 的值;
的值;