题目内容
1.(1)求证:2(1+cosα)-sin2α=4cos4$\frac{α}{2}$;(2)若π<α<$\frac{3π}{2}$,证明$\frac{1+sinα}{\sqrt{1+cosα}-\sqrt{1-cosα}}$+$\frac{1-sinα}{\sqrt{1+cosα}+\sqrt{1-cosα}}$=-$\sqrt{2}$cos$\frac{α}{2}$.
分析 (1)利用1+cosα=2cos2$\frac{α}{2}$及同角三角函数关系式能证明2(1+cosα)-sin2α=4cos4$\frac{α}{2}$.
(2)由π<α<$\frac{3π}{2}$,利用三角函数的图象和性质可得sin$\frac{α}{2}$>0,cos$\frac{α}{2}$<0,利用二倍角公式化简所求证明等式左边等于右边即可得证.
解答 证明:(1)2(1+cosα)-sin2α
=2×2cos2$\frac{α}{2}$-1+cos2α
=4cos2$\frac{α}{2}$-1+(2cos2$\frac{α}{2}$-1)2
=4cos2$\frac{α}{2}$-1+(2cos2$\frac{α}{2}$-1)2+4cos4$\frac{α}{2}$-4cos2$\frac{α}{2}$+1
=4cos4$\frac{α}{2}$.
∴2(1+cosα)-sin2α=4cos4$\frac{α}{2}$.
(2)∵π<α<$\frac{3π}{2}$,∴$\frac{π}{2}$<$\frac{α}{2}$<$\frac{3π}{4}$,
∴sin$\frac{α}{2}$>0,cos$\frac{α}{2}$<0,
∴左边=$\frac{1+sinα}{-\sqrt{2}cos\frac{α}{2}-\sqrt{2}sin\frac{α}{2}}$+$\frac{1-sinα}{-\sqrt{2}cos\frac{α}{2}+\sqrt{2}sin\frac{α}{2}}$
=$\frac{(1+sinα)(cos\frac{α}{2}-sin\frac{α}{2})}{-\sqrt{2}cosα}$+$\frac{(1-sinα)(sin\frac{α}{2}+cos\frac{α}{2})}{-\sqrt{2}cosα}$
=$\frac{2cos\frac{α}{2}-2sinαsin\frac{α}{2}}{-\sqrt{2}cosα}$
=$\frac{\sqrt{2}cos\frac{α}{2}(1-2sin\frac{α}{2})}{-cosα}$
=-$\sqrt{2}$cos$\frac{α}{2}$=右边.
故得证.
点评 本题考查三角函数恒等式的化简证明,解题时要认真审题,注意二倍角公式和同角三角函数关系式的合理运用,注意转化思想的运用,属于中档题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | (x+2)2+y2=4 | B. | (x+2)2+y2=16 | C. | x2+(y+2)2=4 | D. | x2+(y+2)2=16 |
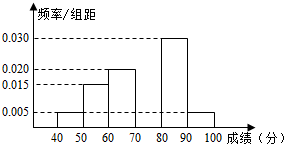 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),