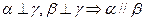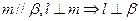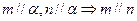题目内容
(本题满分16分)已知在棱长为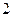 的正方体
的正方体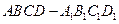 中,
中,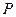 为棱
为棱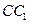 的中点,
的中点,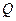 为正方形
为正方形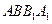 的中心,点
的中心,点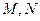 分别在直线
分别在直线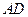 和
和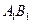 上.
上.
(1)若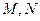 分别为棱
分别为棱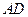 ,
,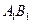 的中点,求直线
的中点,求直线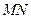 与
与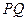 所成角的余弦值;
所成角的余弦值;
(2)若直线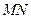 与直线
与直线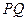 垂直相交,求此时线段
垂直相交,求此时线段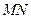 的长;
的长;
(3)在(2)的条件下,求直线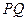 与
与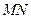 所确定的平面与平面
所确定的平面与平面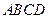 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
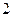 的正方体
的正方体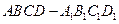 中,
中,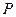 为棱
为棱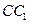 的中点,
的中点,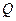 为正方形
为正方形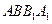 的中心,点
的中心,点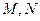 分别在直线
分别在直线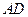 和
和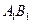 上.
上.
(1)若
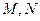 分别为棱
分别为棱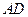 ,
,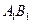 的中点,求直线
的中点,求直线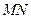 与
与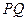 所成角的余弦值;
所成角的余弦值;(2)若直线
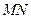 与直线
与直线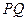 垂直相交,求此时线段
垂直相交,求此时线段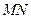 的长;
的长;(3)在(2)的条件下,求直线
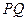 与
与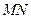 所确定的平面与平面
所确定的平面与平面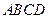 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.(1)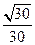
(2)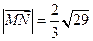
(3)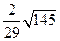
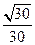
(2)
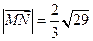
(3)
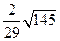
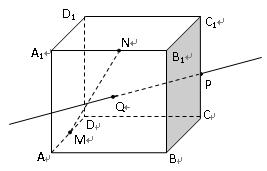
(1)以D为空间直角坐标系的原点,DA所在直线为x轴,DC所在直线为y轴,建立如图所示的空间直角坐标系,则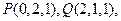
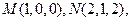
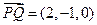 ,
,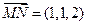 ,……3分
,……3分

设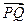 与
与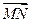 所成的角为
所成的角为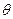 ,
,
则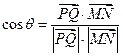
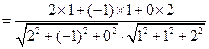
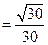
 直线
直线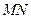 与
与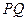 所成角的余弦值为
所成角的余弦值为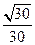 .……………………………………… 5分
.……………………………………… 5分
(2)设点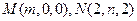 ,则
,则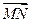 =
=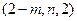 ,
,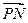 =
=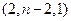 ,
,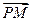 =
=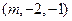 ,
,
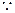
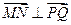
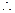
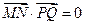 即
即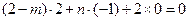
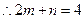 ……⑴……………………………………………………………………8分
……⑴……………………………………………………………………8分
设直线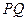 与直线
与直线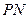 确定平面
确定平面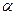 ,其法向量
,其法向量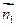 =
=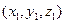 ,
,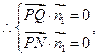
即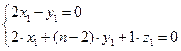 ,令
,令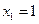 ,得
,得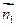 =
=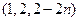
设直线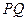 与直线
与直线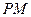 确定平面
确定平面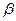 ,其法向量
,其法向量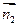 =
=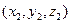 ,
,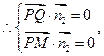
即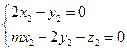 ,令
,令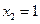 ,得
,得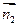 =
=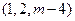
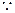
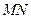 与直线
与直线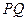 相交,
相交,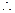
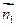 ∥
∥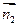
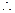
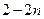 =
=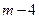 ,……………⑵…………11分
,……………⑵…………11分
由⑴⑵联立方程组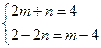 解得,
解得,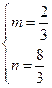 ,
,
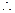
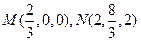 ,
,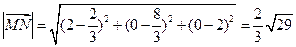 … 13分
… 13分
(本小问也可落实三条直线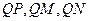 共面的条件得到点
共面的条件得到点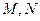 坐标)
坐标)
(3)由(2)得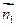 =
=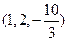 ,平面
,平面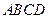 的法向量
的法向量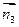 =
=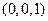 ,
,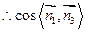 =
=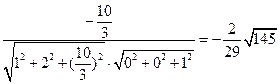
 直线
直线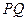 与
与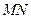 所确定的平面与平面
所确定的平面与平面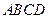 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为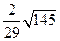
……………………………………………………………………………………… 16分
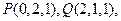
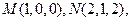
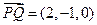 ,
,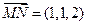 ,……3分
,……3分
设
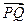 与
与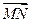 所成的角为
所成的角为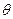 ,
,则
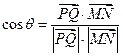
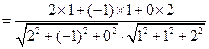
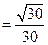
 直线
直线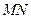 与
与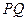 所成角的余弦值为
所成角的余弦值为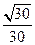 .……………………………………… 5分
.……………………………………… 5分(2)设点
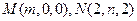 ,则
,则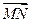 =
=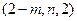 ,
,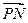 =
=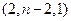 ,
,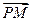 =
=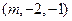 ,
,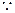
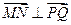
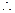
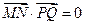 即
即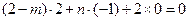
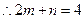 ……⑴……………………………………………………………………8分
……⑴……………………………………………………………………8分设直线
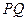 与直线
与直线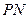 确定平面
确定平面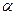 ,其法向量
,其法向量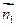 =
=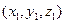 ,
,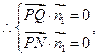
即
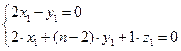 ,令
,令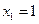 ,得
,得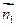 =
=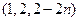
设直线
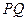 与直线
与直线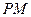 确定平面
确定平面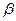 ,其法向量
,其法向量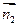 =
=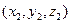 ,
,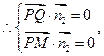
即
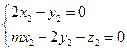 ,令
,令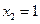 ,得
,得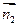 =
=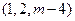
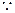
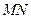 与直线
与直线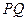 相交,
相交,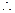
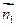 ∥
∥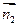
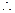
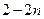 =
=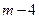 ,……………⑵…………11分
,……………⑵…………11分由⑴⑵联立方程组
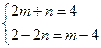 解得,
解得,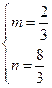 ,
,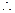
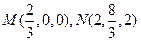 ,
,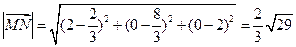 … 13分
… 13分(本小问也可落实三条直线
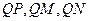 共面的条件得到点
共面的条件得到点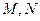 坐标)
坐标)(3)由(2)得
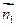 =
=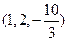 ,平面
,平面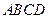 的法向量
的法向量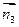 =
=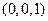 ,
,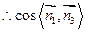 =
=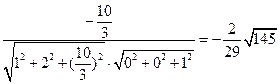
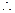 直线
直线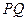 与
与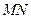 所确定的平面与平面
所确定的平面与平面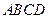 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为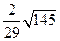
……………………………………………………………………………………… 16分

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
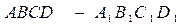 中,求:
中,求: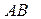 与
与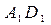 所成的角;
所成的角;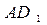 与
与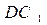 所成的角。
所成的角。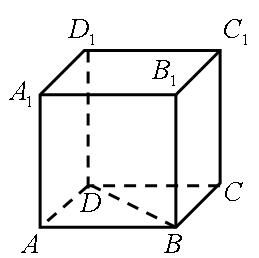
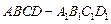 是
是 底面为正方形的长方体,
底面为正方形的长方体,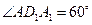 ,
,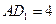 ,点
,点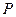 是
是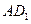 上的动点.
上的动点. 任何位置,是否都有平面
任何位置,是否都有平面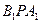 垂直于平面
垂直于平面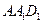 ?并证明你的结论;
?并证明你的结论;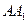 与
与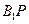 所成角的余弦值;
所成角的余弦值;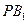 与平面
与平面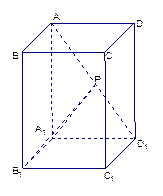
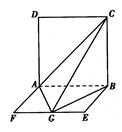
 平面BGC;
平面BGC; 底面ABC,AB=BC,D、F分别为
底面ABC,AB=BC,D、F分别为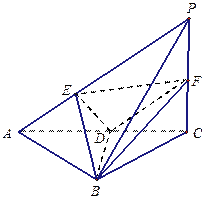
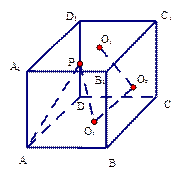
 中,P为DD1中点,O1、O2、O3分别为面
中,P为DD1中点,O1、O2、O3分别为面 、面
、面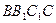 、面
、面 的中心。(1)求证:
的中心。(1)求证: 。
。 中,
中, ,
, ,
, ,
, 是棱
是棱 上一动点,
上一动点, 的最小值为
的最小值为 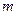 、
、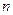 、
、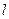 是三条不同的直线,
是三条不同的直线,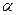 、
、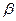 、
、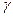 是三个不同的平面,则下列命题正确的是( )
是三个不同的平面,则下列命题正确的是( )