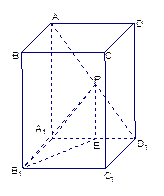
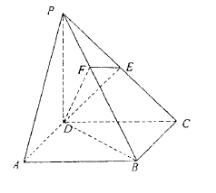
题目内容
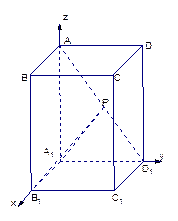
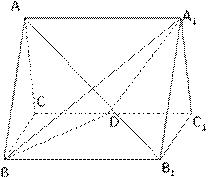
如图,已知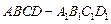 是
是 底面为正方形的长方体,
底面为正方形的长方体,
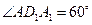 ,
,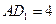 ,点
,点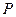 是
是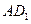 上的动点.
上的动点.
(1)试判断不论点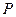 在
在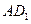 上的
上的 任何位置,是否都有平面
任何位置,是否都有平面
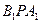 垂直于平面
垂直于平面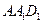 ?并证明你的结论;
?并证明你的结论;
(2)当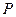 为
为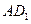 的中点时,求异面直线
的中点时,求异面直线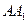 与
与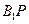 所成角的余弦值;
所成角的余弦值;
(3)求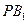 与平面
与平面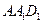
 所成角的正切值的最大值.
所成角的正切值的最大值.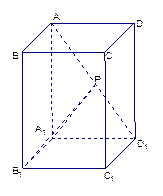
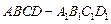 是
是 底面为正方形的长方体,
底面为正方形的长方体,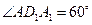 ,
,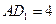 ,点
,点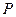 是
是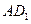 上的动点.
上的动点.(1)试判断不论点
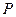 在
在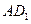 上的
上的 任何位置,是否都有平面
任何位置,是否都有平面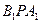 垂直于平面
垂直于平面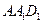 ?并证明你的结论;
?并证明你的结论;(2)当
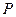 为
为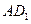 的中点时,求异面直线
的中点时,求异面直线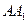 与
与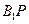 所成角的余弦值;
所成角的余弦值;(3)求
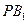 与平面
与平面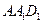
 所成角的正切值的最大值.
所成角的正切值的最大值.
(1)不论点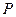 在
在
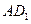 上的任何位置,都有平面
上的任何位置,都有平面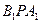 垂直于平面
垂直于平面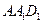 .
.
证明如下:由题意知,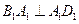 ,
,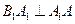 又
又
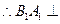 平面
平面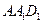 又
又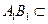 平面
平面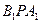
 平面
平面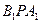
 平面
平面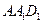
 .
.
(2)解法一:过点P作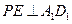 ,垂足为
,垂足为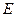 ,连结
,连结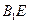 (如图),则
(如图),则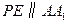 ,
,
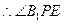 是异面直线
是异面直线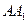 与
与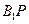 所成的角.
所成的角.
在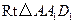 中 ∵
中 ∵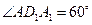 ∴
∴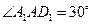
∴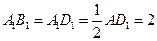 ,
, 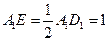 ,
,
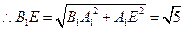 . 又
. 又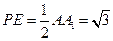 .
.
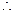 在
在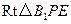 中,
中,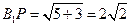
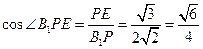 .
.
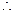 异面异面直线
异面异面直线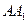 与
与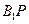 所成角的余弦值为
所成角的余弦值为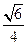 .
.
 解法二:以
解法二:以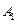 为原点,
为原点,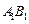 所在的直线为x轴建立空间直角坐标系如图示,则
所在的直线为x轴建立空间直角坐标系如图示,则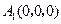 ,
,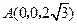 ,
, ,
,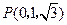 ,
,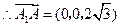 ,
,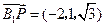
∴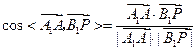
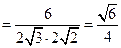 .
.
∴异面异面直线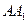 与
与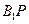 所成角的余弦值为
所成角的余弦值为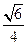 .
.
(3)由(1)知,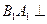 平面
平面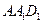
 ,
,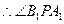 是
是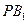 与平面
与平面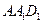 所成的角,
所成的角,
且 .
.
当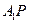 最小时,
最小时,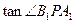 最大,这时
最大,这时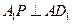 ,由
,由
得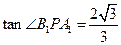 ,即
,即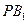 与平面
与平面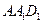 所成角的正切值的最大值
所成角的正切值的最大值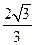 .
.
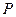 在
在
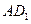 上的任何位置,都有平面
上的任何位置,都有平面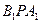 垂直于平面
垂直于平面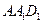 .
.证明如下:由题意知,
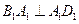 ,
,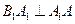 又
又
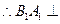 平面
平面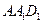 又
又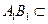 平面
平面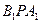
 平面
平面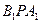
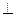 平面
平面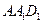
 .
.(2)解法一:过点P作
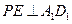 ,垂足为
,垂足为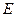 ,连结
,连结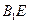 (如图),则
(如图),则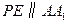 ,
,
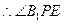 是异面直线
是异面直线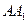 与
与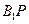 所成的角.
所成的角.在
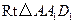 中 ∵
中 ∵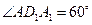 ∴
∴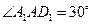
∴
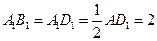 ,
, 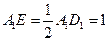 ,
, 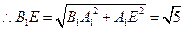 . 又
. 又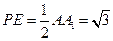 .
. 在
在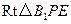 中,
中,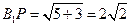
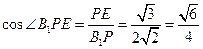 .
. 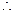 异面异面直线
异面异面直线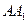 与
与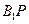 所成角的余弦值为
所成角的余弦值为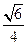 .
. 解法二:以
解法二:以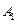 为原点,
为原点,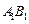 所在的直线为x轴建立空间直角坐标系如图示,则
所在的直线为x轴建立空间直角坐标系如图示,则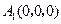 ,
,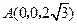 ,
, ,
,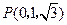 ,
,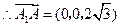 ,
,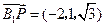
∴
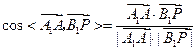
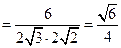 .
.∴异面异面直线
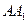 与
与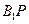 所成角的余弦值为
所成角的余弦值为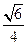 .
.(3)由(1)知,
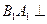 平面
平面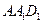
 ,
,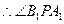 是
是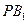 与平面
与平面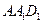 所成的角,
所成的角,且
 .
.当
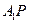 最小时,
最小时,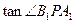 最大,这时
最大,这时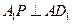 ,由
,由
得
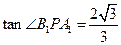 ,即
,即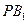 与平面
与平面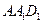 所成角的正切值的最大值
所成角的正切值的最大值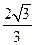 .
.略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 面ABC,BC
面ABC,BC P,使得CP
P,使得CP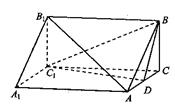
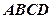 ,
,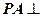 平面
平面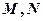 分别是
分别是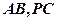 的中点,
的中点,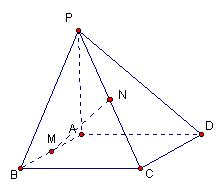
 直线
直线 ,
, 与平面
与平面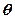 ,能否确定
,能否确定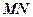 是异面直线
是异面直线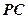 的公垂线.若能确定,求出
的公垂线.若能确定,求出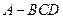 中,
中,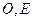 分别是
分别是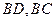 的中点,
的中点,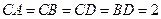 ,
,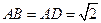 。
。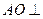 平面
平面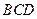 ;
;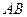 与
与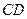 所成角的余弦值;
所成角的余弦值;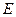 到平面
到平面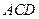 的距离。
的距离。
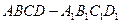 的棱长为
的棱长为 ,
,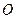 是
是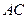 与
与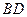 的交点,
的交点,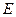 为
为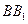 的中点.
的中点.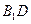 ∥平面
∥平面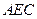 ;
;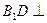 平面
平面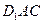 ;
;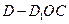 的体积.
的体积.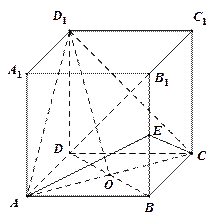
 中,底面
中,底面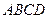 是正方形,侧棱
是正方形,侧棱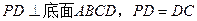 ,
,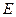 为
为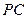 中点,作
中点,作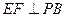 交
交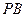 于
于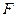
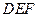 与平面
与平面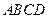 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。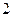 的正方体
的正方体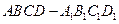 中,
中,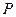 为棱
为棱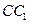 的中点,
的中点,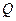 为正方形
为正方形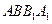 的中心,点
的中心,点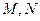 分别在直线
分别在直线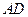 和
和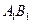 上.
上.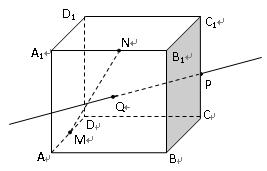
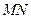 与
与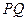 所成角的余弦值;
所成角的余弦值;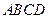 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.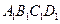 中心为
中心为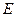 ,
,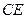 垂直,这样的直线可画
垂直,这样的直线可画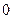 条
条 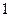 条
条 条
条 