Question

对于实数a和b，定义运算“?”：a?b=

a2-ab， a≤b b2-ab， a＞b

，设f（x）=（3x-1）?（x-1）．且关于x的方程f（x）=m恰有三个不相等的实数根x₁，x₂，x₃，则x₁+x₂+x₃的取值范围是

 

．

Answer 1

考点：根的存在性及根的个数判断

专题：计算题,作图题,函数的性质及应用

分析：由题意首先化简函数f（x）=

2x(3x-1)，x≤0 -2x(x-1)，x＞0

；从而作函数的图象辅助求解．

解答： 解：由题意，
当x≤0时，3x-1≤x-1；
则f（x）=（3x-1）?（x-1）
=（3x-1）（3x-1-x+1）
=2x（3x-1）；
当x＞0时，3x-1＞x-1；
则f（x）=（3x-1）?（x-1）
=（x-1）（-3x+1+x-1）
=-2x（x-1）；
则f（x）=

2x(3x-1)，x≤0 -2x(x-1)，x＞0

；
作函数f（x）=

2x(3x-1)，x≤0 -2x(x-1)，x＞0

的图象如下，

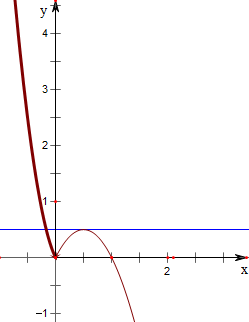
不妨设x₁＜x₂＜x₃，易知x₂+x₃=1；
而由0＜2x₁（3x₁-1）＜

1

2

及x₁＜0解得，
-

1

6

＜x₁＜0；
故

5

6

＜x₁+x₂+x₃＜1；
故答案为：（

5

6

，1）．

点评：本题考查了学生对新定义的接受能力及函数的化简，属于基础题．