题目内容
19.设a=log${\;}_{\frac{2}{3}}$$\frac{3}{2}$,b=log32,c=2${\;}^{\frac{1}{3}}$,d=3${\;}^{\frac{1}{2}}$,则这四个数的大小关系是( )| A. | a<b<c<d | B. | a<c<d<b | C. | b<a<c<d | D. | b<a<d<c |
分析 利用对数函数、指数函数的单调性求解.
解答 解:∵a=log${\;}_{\frac{2}{3}}$$\frac{3}{2}$<$lo{g}_{\frac{2}{3}}1$=0,0=log31<b=log32<log33=1,
$c={2^{\frac{1}{3}}}>1$,$d={3^{\frac{1}{2}}}>1$,
又由${c^6}={({2^{\frac{1}{3}}})^6}=4$,${d^6}={({3^{\frac{1}{2}}})^6}=9$,知d>c,
∴a<b<c<d.
故选:A.
点评 本题考查四个数的大小的比较,是基础题,解题时要认真审题,注意对数函数、指数函数的单调性的合理运用.

练习册系列答案
相关题目
9.一个几何体的三视图如图所示,则该几何体的表面积为( )
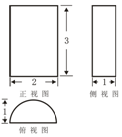

| A. | 4π | B. | 5π+6 | C. | 3π+6 | D. | 4π+6 |
7.已知f(x)、g(x)、h(x)均为一次函数,若对实数x满足:|f(x)|+|g(x)|+h(x)=$\left\{\begin{array}{l}{4x+2}&{x≥2}\\{未知}&{-\frac{1}{2}≤x<2}\\{-2x+4}&{x<-\frac{1}{2}}\end{array}\right.$,则h(x)的解析式为( )
| A. | 2x+6 | B. | 6x-2 | C. | 3x-1 | D. | x+3 |
14.直线y=kx+1-k与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
4.执行如图的程序框图,若输出的$S=\frac{31}{32}$,则输入的整数p的值为( )


| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
11.若函数y=x2-mx+1在区间[1,2]上单调递增,则实数m的取值范围是( )
| A. | (-∞,2] | B. | (-∞,2) | C. | (4,+∞) | D. | [4,+∞) |