Question

已知椭圆C的焦点F₁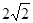（－，0）和F₂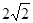（，0），长轴长6。

(1)求椭圆C的标准方程。

(2)设直线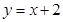交椭圆C于A、B两点，求线段AB的中点坐标。

 

Answer 1

【答案】

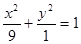（1）（2）。

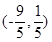【解析】

试题分析：（1）由F₁（－，0）和F₂（，0），长轴长为6得：c=2，a=3，所以b=1。所以椭圆方程为。

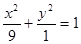（2）设A()B(),由（1）可知椭圆方程为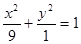  ，与直线AB的方程y=x+2联立化简并整理得10x²+36x+27=0，∴x₁+x₂=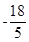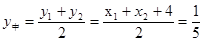，，。所以AB的中点的坐标为。

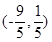考点：本题考查直线与圆锥曲线的综合问题；椭圆的标准方程；中点坐标公式。

点评：此题的第二问也可以用点差法，一般情况下，遇到弦中点的问题可以先考虑点差法。