题目内容
19.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的2×2列联表:| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过5%的前提下,认为“该市居民能否做到‘光盘’与性别有关” | |
| B. | 在犯错误的概率不超过2.5%的前提下,认为“该市居民能否做到‘光盘’与性别有关” | |
| C. | 有90%以上的把握认为“该市居民能否做到‘光盘’与性別无关” | |
| D. | 有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关” |
分析 计算K2,参照附表得出正确的结论.
解答 解:经计算K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{100{×(45×15-30×10)}^{2}}{55×45×75×25}$≈3.030>2.706,
参照附表,得到的正确结论是有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”.
故选:D.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
13.如果P,P2,…Pn是抛物线C=y2=8x上的点,它们的横坐标依次为:x1,x2,…,xn,F是抛物线C的焦点,若x1+x2+…+xn=2017,|P1F|+|P2F|+…+|PnF|=( )
| A. | n+2017 | B. | n+4034 | C. | 2n+2017 | D. | 2n+4034 |
10.复数$\frac{1+i}{i}$的虚部是( )
| A. | -i | B. | 1 | C. | -1 | D. | i |
7.以下程序运行的结果是( )
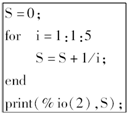
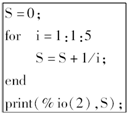
| A. | $\frac{137}{60}$ | B. | $\frac{133}{60}$ | C. | $\frac{131}{60}$ | D. | $\frac{121}{60}$ |
14.已知函数f(x)的部分图象如图所示,则f(x)的解析式可能是( )


| A. | f(x)=$\frac{sin2x}{{x}^{2}}$ | B. | f(x)=$\frac{cos2x}{{x}^{2}}$ | C. | f(x)=$\frac{co{s}^{2}x}{2x}$ | D. | f(x)=$\frac{cos2x}{x}$ |
4.复数1-$\frac{i}{3+i}$等于( )
| A. | $\frac{9}{10}$-$\frac{3}{10}$i | B. | $\frac{1}{10}$+$\frac{3}{10}$i | C. | $\frac{9}{10}$+$\frac{3}{10}$i | D. | $\frac{1}{10}$-$\frac{3}{10}$i |
11.已知a,b,c,d是四条不同的直线,且a,b是异面直线,则下面说法正确的是( )
| A. | 若c,d 与a,b都相交,则c,d是异面直线 | |
| B. | 若c∥a,d∥b,则 c,d 是异面直线 | |
| C. | 若c,d 与 a,b 都异面,则 c,d 是异面直线 | |
| D. | 若c,d 与 a,b 都垂直,则 c∥d |