题目内容
如图,椭圆长轴的端点为A,B,O为椭圆的中心,F为椭圆的右焦点,且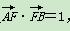 ,
,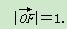 .
.
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为M,直线l交椭圆于P,Q两点,问:是否存在直线l,使点F恰为△PQM的垂心,若存在,求出直线l的方程;若不存在,请说明理由.
解 (1)设椭圆方程为 +
+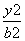 =1(a>b>0),则c=1,
=1(a>b>0),则c=1,
又∵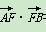 =(a+c)·(a-c)=a2-c2=1.
=(a+c)·(a-c)=a2-c2=1.
∴a2=2,b2=1.
故椭圆的方程为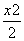 +y2=1.
+y2=1.
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,设P(x1,y1),Q(x2,y2),
∵M(0,1),F(1,0),∴直线l的斜率k=1.
于是设直线l为y=x+m,由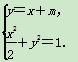
得3x2+4mx+2m2-2=0,
x1+x2=-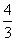 m,①
m,①
x1x2=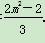 .②
.②
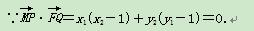 又yi=xi+m(i=1,2),
又yi=xi+m(i=1,2),
∴x1(x2-1)+(x2+m)(x1+m-1)=0,
即2x1x2+(x1+x2)(m-1)+m2-m=0.
将①②代入得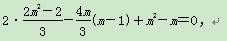
解得m=-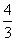 或m=1,经检验m=-
或m=1,经检验m=-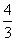 符合条件.
符合条件.
故存在直线l,使点F恰为△PQM的垂心,直线l的方程为y=x-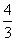 .
.

某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气 质量 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中重度 污染 | 重度 污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系为:
S=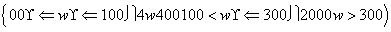 试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染.完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
| 非重度污染 | 重度污染 | 合计 |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 |
|
| 100 |
附:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
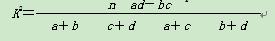
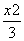 +y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )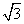 B.6
B.6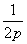 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: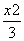 -y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )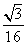 B.
B.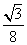
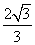 D.
D.
 (a>0),且满足条件sinC-sinB=
(a>0),且满足条件sinC-sinB= sinA,则动点A的轨迹方程是________.
sinA,则动点A的轨迹方程是________.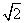
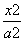 +
+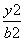 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为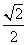 ,且过点(2,
,且过点(2,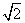 ).
).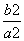 .
.