题目内容

已知离心率为 $数学公式$ 的椭圆C₁： $数学公式$ （a＞b＞0）的左右焦点分别为F₁、F₂，椭圆C₁与抛物线C₂：y²=-x的交点的横坐标为
-2．
（1）求椭圆的标准方程；
（2）如果直线l：y=kx+m与椭圆相交于P₁、P₂两点，设直线P₁F₁与P₂F₁的倾斜角分别为α，β，当α+β=π时，求证：直线l必过定点．

解：（1）由于 $\text{[math]}$ ， $\text{[math]}$ ，a²=2b²
又因y²=-x的交点的横坐标为-2，y²=2，代入 $\text{[math]}$ ，
∴a²=8
所以椭圆方程为 $\text{[math]}$
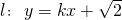
（2）联立 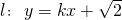$\text{[math]}$ 与y=kx+m得到（2k²+1）x²+4mkx+2m²-8=0 $\text{[math]}$
设直线P₁F₁与P₂F₁的倾斜角分别为α，β，
当α+β=π时，若设 $\text{[math]}$
k₁=tanα，k₂=tanβ=tan（π-α）=-tanα=-k₁，
∴k₁+k₂=0
$\text{[math]}$ ， $\text{[math]}$
k₁+k₂= $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$
= $\text{[math]}$
= $\text{[math]}$
所以 m=4k
直线方程为 y=kx+4k=k（x+4），
故直线过定点（-4，0）
分析：（1）利用椭圆的离心率的值，得到椭圆中参数的关系，利用椭圆C₁与抛物线C₂：y²=-x的交点的横坐标为-2，代入抛物线的方程，求出交点的坐标，代入椭圆方程求出参数值，即得到椭圆的方程．
（2）将直线的方程与椭圆的方程联立，利用韦达定理，得到交点的坐标满足的条件，将已知条件α+β=π转化为两条直线的斜率满足k₁+k₂=0，将斜率用坐标表示，得到 m=4k，代入直线的方程，判断出直线过定点．
点评：解决直线与圆锥曲线的相交的有关问题，一般的思路是将直线与圆锥曲线方程联立，得到关于应该未知数的方程，利用韦达定理来解决．属于难题，计算量大．