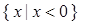题目内容
已知数列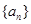 的前
的前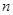 项和为
项和为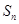 ,函数
,函数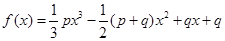 (其中
(其中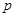 ,
,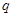 为常数且
为常数且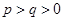 )
)
(1)若当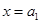 时,函数
时,函数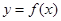 取得极大值,求
取得极大值,求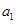 的值;
的值;
(2)若当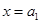 时,函数
时,函数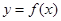 取得极小值,点
取得极小值,点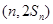 ,
,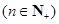 都在函数
都在函数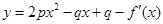 的图像上,(
的图像上,(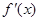 是
是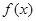 的导函数),求数列
的导函数),求数列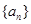 的通项公式.
的通项公式.
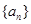 的前
的前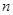 项和为
项和为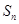 ,函数
,函数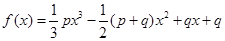 (其中
(其中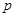 ,
,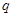 为常数且
为常数且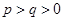 )
)(1)若当
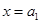 时,函数
时,函数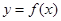 取得极大值,求
取得极大值,求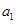 的值;
的值;(2)若当
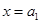 时,函数
时,函数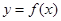 取得极小值,点
取得极小值,点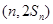 ,
,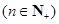 都在函数
都在函数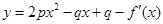 的图像上,(
的图像上,(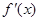 是
是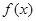 的导函数),求数列
的导函数),求数列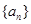 的通项公式.
的通项公式.(1)
(2)

(2)

解:(1)
由 得
得  ,
,
∵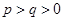 ∴
∴
 随x变化而变化如下表
随x变化而变化如下表
∴当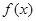 取得极大值时
取得极大值时 6分
6分
(2)由上表得 时
时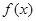 取得极小值.
取得极小值.

点 在其函数图象x
在其函数图象x
n=1时 点(1,2)在函数图象上
点(1,2)在函数图象上

 时
时  (1)
(1)
 (2)
(2)
(1)—(2)得
当n=1时也符合上式∴
 12分
12分

由
 得
得  ,
,
∵
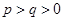 ∴
∴
 随x变化而变化如下表
随x变化而变化如下表| x |  |  | ( ,1) ,1) | 1 |  |
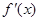 | + | 0 | — | 0 | + |
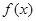 | ↗ | 极大植 | ↘ | 极小值 | ↗ |
∴当
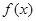 取得极大值时
取得极大值时 6分
6分(2)由上表得
 时
时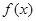 取得极小值.
取得极小值.
点
 在其函数图象x
在其函数图象xn=1时
 点(1,2)在函数图象上
点(1,2)在函数图象上
 时
时  (1)
(1) (2)
(2)(1)—(2)得

当n=1时也符合上式∴

 12分
12分
练习册系列答案
相关题目

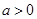 ,讨论
,讨论 的单调性;
的单调性;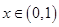 恒有
恒有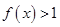 ,求
,求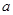 的取值范围
的取值范围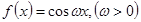 将
将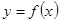 的图象向右平移
的图象向右平移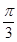 个单位长
个单位长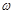 的最小值等于( )
的最小值等于( )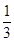
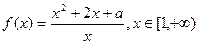
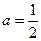 时,求函数
时,求函数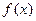 的最小值;
的最小值;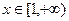 ,
,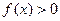 恒成立,试求实数
恒成立,试求实数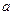 的取值范围.
的取值范围.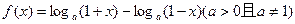
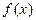 的奇偶性与单调性;
的奇偶性与单调性;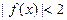 的解集为
的解集为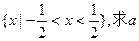 的值;
的值; (x+
(x+ -a)的定义域为A,值域为B.
-a)的定义域为A,值域为B. 知二次函数
知二次函数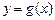 的图象经过点
的图象经过点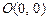 、
、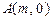 与点
与点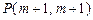 ,设函数
,设函数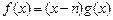 在
在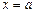 和
和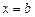 处取到极值,其中
处取到极值,其中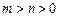 ,
,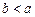 。
。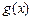 的二次项系数
的二次项系数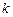 的值;
的值;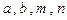 的大小(要求按从小到大排列);
的大小(要求按从小到大排列);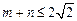 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线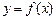 均相切,求
均相切,求 的定义域是:
的定义域是:



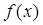 是偶函数,当
是偶函数,当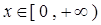 时,
时,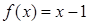 ,则
,则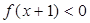 解集为:
解集为: