题目内容
10.若工人月工资(元)依劳动产值(万元)变化的回归直线方程为$\stackrel{∧}{y}$=60+90x,则下列说法正确的是③(填序号).①劳动产值为10000元时,工资为50元;
②劳动产值提高10000元时,工资提高150元;
③劳动产值提高10000元时,工资提高90元;
④劳动产值为10000元时,工资为90元.
分析 根据所给的线性回归方程,当x增加1时,y要增加90元,当劳动效率增加1000元时,工资提高90元,这里的值是平均增加90元.
解答 解:∵回归直线方程为$\stackrel{∧}{y}$=60+90x,
∴当x增加1时,y要增加90元,
∴当劳动效率增加1000元时,工资提高90元,
故答案为:③.
点评 本题考查线性回归方程的应用,解题的关键是看清题目中自变量的值每增加1个单位,y的值就平均增加90,注意平均一词.

练习册系列答案
相关题目
20.已知cos(π-α)=-$\frac{5}{13}$且α是第一象限角,则sinα=( )
| A. | $-\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $-\frac{12}{13}$ | D. | $\frac{5}{13}$ |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为10,一条渐近线为y=$\frac{1}{2}$x,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}$=1 | C. | $\frac{{x}^{2}}{80}-\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{80}$=1 |
5.若sinα=$\frac{4}{5}$,且α为锐角,则tanα的值等于( )
| A. | $\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
15.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$•$\overrightarrow{b}$的值为( )
| A. | -4 | B. | 8 | C. | -1 | D. | -7 |
2.若直线l1:(m-2)x-y-1=0,与直线l2:3x-my=0互相平行,则m的值等于( )
| A. | 0或-1或3 | B. | 0或3 | C. | 0或-1 | D. | -1或3 |
19.执行如图所示的程序框图,当输入x为16时,输出的y=( )
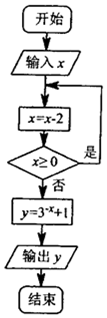

| A. | 28 | B. | 10 | C. | 4 | D. | 2 |
20.函数f(x)=$\frac{1}{2}$x2-lnx,在(1,$\frac{1}{2}$)处的切线斜率为( )
| A. | 1 | B. | 2 | C. | 0 | D. | $\frac{1}{2}$ |