题目内容
20.已知全集U=R,集合A={x|lgx≥0},$B=\left\{{x\left|{{2^x}≥\sqrt{2}}\right.}\right\}$,则A∩B为( )| A. | {x|x≥1} | B. | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | C. | {x|0<x≤1} | D. | $\left\{{x\left|{0<x≤\frac{1}{2}}\right.}\right\}$ |
分析 分别求出A与B中不等式的解集确定出A与B,找出两集合的交集即可.
解答 解:由A中不等式lgx≥0=lg1,
得到x≥1,即A={x|x≥1},
由B中不等式变形得:2x≥$\sqrt{2}$=2${\;}^{\frac{1}{2}}$,即x≥$\frac{1}{2}$,
∴B={x|x≥$\frac{1}{2}$},
则A∩B={x|x≥1},
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
10.一个蜂巢里有1只蜜蜂,第一天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,…,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有( )只蜜蜂.
| A. | 972 | B. | 1456 | C. | 4096 | D. | 5460 |
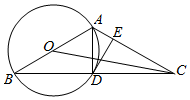 如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.
如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.