题目内容
已知sin(θ-
)=
,θ∈(0,π),则cosθ= .
| π |
| 3 |
| ||
| 2 |
考点:两角和与差的正弦函数,三角函数的化简求值
专题:三角函数的求值
分析:首先,结合给定的角的范围,和已知条件,得到θ-
=
或
,然后,求解即可得到结果.
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解答:
解:∵θ∈(0,π),
∴(θ-
)∈(-
,
),
∵sin(θ-
)=
>0,
∴θ-
=
或
,
∴θ=
或π,
∴cosθ=-
或-1,
故答案为:-
或-1.
∴(θ-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∵sin(θ-
| π |
| 3 |
| ||
| 2 |
∴θ-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴θ=
| 2π |
| 3 |
∴cosθ=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题重点考查了特殊角的三角函数等知识,属于中档题.

练习册系列答案
相关题目
若不等式组
表示的平面区域经过所有四个象限,则实数λ的取值范围是( )
|
| A、(-∞,4)?? |
| B、[1,2] |
| C、(1,4) |
| D、(1,+∞)? |
已知数列{an}是公比为2的等比数列,若a3a4a5=8,则a6等于( )
| A、4 | B、8 | C、12 | D、16 |
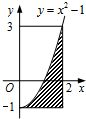 如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},向区域D内任投一点,记此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )
如图,设区域D={(x,y)|0≤x≤2,-1≤y≤3},向区域D内任投一点,记此点落在阴影区域M={(x,y)|0≤x≤2,-1≤y≤x2-1}的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
若函数g(x)=xm+ax的导函数为g'(x)=2x+1,则数列{
}(n∈N*)的前n项和是( )
| 1 |
| g(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数 f(x)=3x+x-5,则函数 f(x)的零点一定在区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
曲线y=exlnx在x=1处的切线方程是( )
| A、y=2e(x-1) |
| B、y=ex-1 |
| C、y=x-e |
| D、y=e(x-1) |