题目内容
若不等式组
表示的平面区域经过所有四个象限,则实数λ的取值范围是( )
|
| A、(-∞,4)?? |
| B、[1,2] |
| C、(1,4) |
| D、(1,+∞)? |
考点:二元一次不等式(组)与平面区域
专题:数形结合
分析:由约束条件作出可行域,结合不等式组
表示的平面区域经过所有四个象限可得λ-1>0,由此求得实数λ的取值范围.
|
解答:
解:由约束条件
作出可行域如图,

则λ-1>0,即λ>1.
∴实数λ的取值范围是(1,+∞).
故选:D.
|

则λ-1>0,即λ>1.
∴实数λ的取值范围是(1,+∞).
故选:D.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
存在实数a使得方程cosx=a在[0,2π]上有两个不相等的实数根x1,x2,则sin
=( )
| x1+x2 |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知f(x)=ax+
+2-2a(a>0),若f(x)≥2lnx在[1,+∞)上恒成立,则a的取值范围是( )
| a-2 |
| x |
| A、(1,+∞) |
| B、[1,+∞) |
| C、(2,+∞) |
| D、[2,+∞) |
执行如图所示的程序框图,若p=0.7,则输出的n为( )


| A、2 | B、3 | C、4 | D、5 |
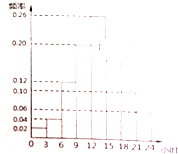 天猫电器城对TCL官方旗舰店某款4K超高清电视机在2014年11月11日的销售情况进行了统计,如图所示,数据显示,该日TCL官方旗舰店在[0,3)小时销售了该款电视机2台.
天猫电器城对TCL官方旗舰店某款4K超高清电视机在2014年11月11日的销售情况进行了统计,如图所示,数据显示,该日TCL官方旗舰店在[0,3)小时销售了该款电视机2台. 如图,已知AB⊥平面BCE,CD∥AB,△BCE是正三角形,AB=BC=2CD.
如图,已知AB⊥平面BCE,CD∥AB,△BCE是正三角形,AB=BC=2CD.