题目内容
7．若集合M={x|y=ln（x-1）}，N={x|y=$\sqrt{2-x}$}，则M∩N=（ ）| A． | {x|1＜x≤2} | B． | {x|1≤x≤2} | C． | {x|x＞1} | D． | {x|1≤x≤2} |
分析 求出M与N中x的范围确定出M与N，找出两集合的交集即可．
解答 解：由M中y=ln（x-1），得到x-1＞0，即x＞1，
∴M={x|x＞1}，
由N中y=$\sqrt{2-x}$，得到2-x≥0，即x≤2，
∴N={x|x≤2}，
则M∩N={x|1＜x≤2}，
故选：A．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
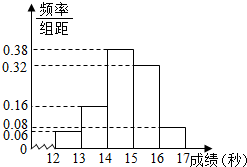某学校高三年级800名学生在一次百米测试中，成绩全部在12秒到17秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[12，13），第二组[13，14），…，第五组[16，17]，如图是根据上述分组得到的频率分布直方图．
18．直线y=2x-1和圆O2：x2+y2-4y=0的位置关系是（ ）
| A． | 相离 | B． | 相交 | C． | 外切 | D． | 内切 |