题目内容
分已知函数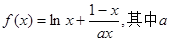 为大于零的常数。
为大于零的常数。
(1)若函数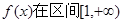 内单调递增,求a的取值范围;
内单调递增,求a的取值范围;
(2)求函数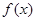 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
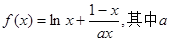 为大于零的常数。
为大于零的常数。(1)若函数
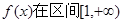 内单调递增,求a的取值范围;
内单调递增,求a的取值范围;(2)求函数
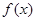 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。(1)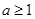
(2)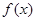 在[1,2]上的最小值为
在[1,2]上的最小值为
①当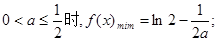
②当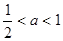 时,
时,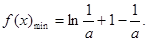
③当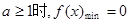
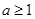
(2)
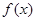 在[1,2]上的最小值为
在[1,2]上的最小值为①当
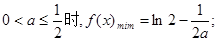
②当
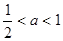 时,
时,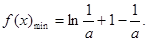
③当
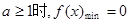
试题分析:解:
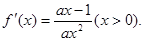 .2分
.2分(1)由已知,得
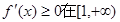 上恒成立,
上恒成立,即
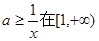 上恒成立
上恒成立又
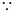 当
当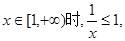
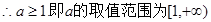 .6分
.6分(2)当
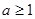 时,
时,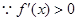 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时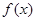 在[1,2]上为增函数
在[1,2]上为增函数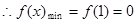
当
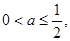
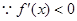 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时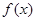 在[1,2]上为减函数
在[1,2]上为减函数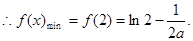
当
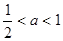 时,令
时,令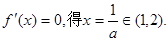
又
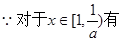
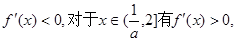
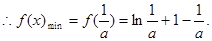
综上,
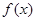 在[1,2]上的最小值为
在[1,2]上的最小值为①当
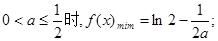
②当
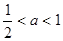 时,
时,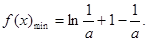
③当
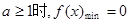 12分
12分点评:主要是考查了导数的符号与函数单调性关系的运用,以及利用分类讨论思想来得到最值,属于基础题。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
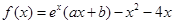 ,曲线
,曲线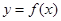 在点
在点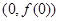 处切线方程为
处切线方程为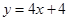 。
。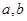 的值;
的值;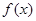 的单调性,并求
的单调性,并求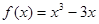
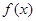 的单调区间;
的单调区间;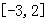 上的最值.
上的最值.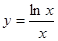 的最大值为( )
的最大值为( )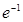

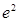
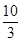
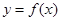 在(
在(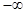 ,+
,+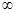 )内有意义.对于给定的正数K,已知函数
)内有意义.对于给定的正数K,已知函数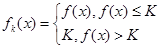 ,取函数
,取函数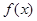 =
=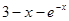 .若对任意的
.若对任意的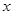
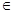 (
(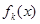 =
=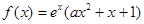 ,
,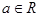 ;
;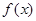 的单调性;
的单调性;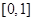 上的最大值为
上的最大值为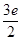 ,求
,求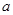 的值.
的值.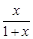 .
.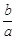 .
.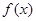
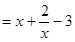 的零点的个数为 .
的零点的个数为 .