已知3m=5n=k且$\frac{1}{m}+\frac{1}{n}=2$.则k的值为$\sqrt{15}$．题目和参考答案——青夏教育精英家教网—

题目内容

13．已知3^m=5ⁿ=k且$\frac{1}{m}+\frac{1}{n}=2$，则k的值为$\sqrt{15}$．

分析利用指数与对数的互化，求出m，n，然后化简求解即可．

解答解：3^m=5ⁿ=k，
可得$\frac{1}{m}$=log_k3，$\frac{1}{n}$=log_k5，
∵$\frac{1}{m}+\frac{1}{n}=2$，
∴log_k3+log_k5=2，
可得log_k15=2，
k=$\sqrt{15}$．
故答案为：$\sqrt{15}$．

点评本题考查指数与对数的互化，考查计算能力．

练习册系列答案

4．在等比数列{a_n}中，a₂=3，a₅=81．
（1）求a₁与公比q；
（2）求数列{a_n}的通项公式a_n；
（3）设b_n=log₃a_n，求数列{b_n}的前n项和S_n．

1．用数学归纳法证明：1×2+2×3+3×4+…+n×（n+1）=$\frac{n（n+1）（n+2）}{3}（n∈{N^*}）$．

8．数列-1，3，-7，15，…的通项公式a_n等于（　　）

（-1）ⁿ⁺¹（2ⁿ-1）

（-1）ⁿ2ⁿ+1

2ⁿ-1

18．设函数f（x）=$\sqrt{3}$sinωx+cosωx-1（ω＞0），且满足相邻两个最大值间的距离为π；
（1）求ω
（2）若y=f（x）的图象向右平移a（a＞0）个单位，图象再向上移动一个单位得到y=g（x）的图象，且y=g（x）为奇函数，求a的最小值．

5．计算$cos\frac{π}{3}$-$tan\frac{π}{4}$+$\frac{3}{4}ta{n^2}\frac{π}{6}$-$sin\frac{π}{6}$+$co{s^2}\frac{π}{6}$的结果为（　　）

A．

-$\frac{1}{2}$

B．

$\frac{{\sqrt{3}-1}}{2}$

C．

D．

$\frac{{\sqrt{3}}}{2}$

2．

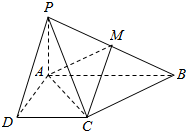已知四棱锥P-ABCD的底面ABCD为直角梯形，AB∥CD，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=$\frac{1}{2}$AB=1，M是PB的中点．
（1）求异面直线AC与PB所成的角的余弦值；
（2）求直线BC与平面ACM所成角的正弦值．

3．方程x³-3x+c=0恰有两个实数根，则c=（　　）

试题分类