题目内容
已知[x]表示不超过x的最大整数,如:[-0.1]=-1,[0.5]=0,现从[log31],[log32],[log33],[log34],…,[log381]中任取一个数,其中该数为奇数的概率为
- A.

- B.
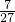
- C.

- D.

A
分析:根据题意,由[x]的意义,分析可得[log31],[log32],[log33],[log34],…,[log381]的值,即可得其中值为奇数的数的个数,由等可能事件的概率公式,计算可得答案.
解答:根据题意,在[log31],[log32],[log33],[log34],…,[log381],共81个数,
其中[log31]=[log32]=0,有2个数等于0;
[log33]=[log34]=…=[log38]=1,有6个数等于1;
[log39]=[log310]=…=[log326]=2,有18个数等于2;
[log327]=[log328]=…=[log380]=3,有54个数等于3;
[log381]=4,有1个数等于4;
该数为奇数的有6+54=60个,
则从[log31],[log32],[log33],[log34],…,[log381]中任取一个数,其中该数为奇数的概率P=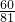 =
= ;
;
故选A.
点评:本题考查等可能事件的概率计算,解题的关键是理解[x]的意义,由对数的性质,得到[log31],[log32],[log33],[log34],…,[log381]的值.
分析:根据题意,由[x]的意义,分析可得[log31],[log32],[log33],[log34],…,[log381]的值,即可得其中值为奇数的数的个数,由等可能事件的概率公式,计算可得答案.
解答:根据题意,在[log31],[log32],[log33],[log34],…,[log381],共81个数,
其中[log31]=[log32]=0,有2个数等于0;
[log33]=[log34]=…=[log38]=1,有6个数等于1;
[log39]=[log310]=…=[log326]=2,有18个数等于2;
[log327]=[log328]=…=[log380]=3,有54个数等于3;
[log381]=4,有1个数等于4;
该数为奇数的有6+54=60个,
则从[log31],[log32],[log33],[log34],…,[log381]中任取一个数,其中该数为奇数的概率P=
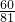 =
= ;
;故选A.
点评:本题考查等可能事件的概率计算,解题的关键是理解[x]的意义,由对数的性质,得到[log31],[log32],[log33],[log34],…,[log381]的值.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知[x]表示不超过x的最大整数,则[log21]+[log22]+[log23]+…[log22009]的值为( )
| A、18054 | B、18044 | C、17954 | D、17944 |