题目内容
把一个体积为27cm3,表面涂有红色油漆的正方体木块锯成27个体积为1cm3的小正方体木块,从中任取1快,则取出的小正方体木块恰有两面涂有油漆的概率为 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:根据正方体的结构,计算出小正方体木块恰有两面涂有油漆的个数,利用公式求出即可.
解答:
解:由正方体的结构及锯木块的方法,
可知不带红漆的只有中间1块,
一面带有红漆的木块是每个面的中间那块,共有6个,
三面带有红漆的木块是每个角上那块,共有8个,
∴两面带有红漆的木块个数m=27-1-6-8=12,
∴取出的小正方体木块恰有两面涂有油漆的概率:
p=
=
.
故答案为:
.
可知不带红漆的只有中间1块,
一面带有红漆的木块是每个面的中间那块,共有6个,
三面带有红漆的木块是每个角上那块,共有8个,
∴两面带有红漆的木块个数m=27-1-6-8=12,
∴取出的小正方体木块恰有两面涂有油漆的概率:
p=
| 12 |
| 27 |
| 4 |
| 9 |
故答案为:
| 4 |
| 9 |
点评:本题考查根据实际情况求事件发生的概率,概率与几何体结合考查,是近几年高考的一个热点,即考查了概率的基础知识,也考查了立体几何的空间想像能力,学习时要注意这两个知识点之间的衔接,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过函数y=sinx图象上一点O(0,0)作切线,则切线方程为( )
| A、y=x | B、y=0 |
| C、y=x+1 | D、y=-x+1 |
下面结论正确的是( )
A、若a<b,则有
| ||||
B、若a>b,则有
| ||||
| C、若a>b,则有a+c>b+c | ||||
| D、若a>b,则|a|>b |
已知等比数列{an}的各项都是正数,且a3-a2=10,a1+a2+a3=35,则数列{an}的前6项和为( )
| A、155 | B、160 |
| C、315 | D、320 |
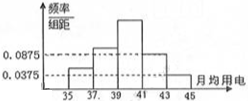 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图.其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图.其中直方图从左到右前3个小矩形的面积之比为1:2:3.