题目内容
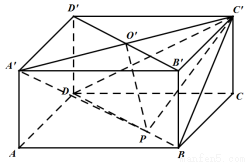
(本小题满分10分)如图,在长方体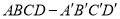 中,
中,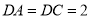 ,
,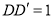 ,
,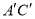 与
与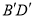 相交于点
相交于点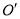 ,点
,点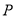 在线段
在线段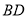 上(点
上(点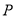 与点
与点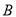 不重合).
不重合).
(1)若异面直线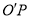 与
与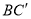 所成角的余弦值为
所成角的余弦值为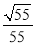 ,求
,求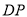 的长度;
的长度;
(2)若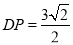 ,求平面
,求平面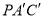 与平面
与平面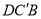 所成角的正弦值.
所成角的正弦值.
(1)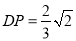 或
或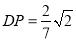 . (2)
. (2)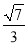
【解析】
试题分析:(1)先建立空间直角坐标系,设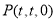 ,利用空间向量数量积可求两向量夹角:
,利用空间向量数量积可求两向量夹角: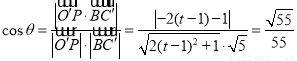 ,解得
,解得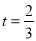 或
或 ,因此
,因此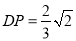 或
或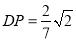 .
.
(2)求二面角,关键求出平面的法向量,设平面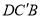 的一个法向量为
的一个法向量为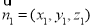 ,根据
,根据 ,可得
,可得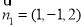 ,同理设平面
,同理设平面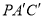 的一个法向量为
的一个法向量为 ,根据
,根据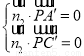 可得
可得 ,因此二面角满足:
,因此二面角满足: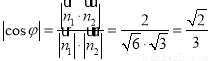 ∴
∴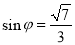 .
.
试题解析:(1)以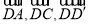 为一组正交基底,建立如图所示的空间直角坐标系
为一组正交基底,建立如图所示的空间直角坐标系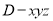 ,
,
由题意,知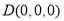 ,
,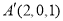 ,
,
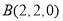 ,
,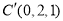 ,
,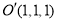 .设
.设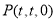 ,
,
∴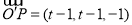 ,
,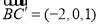 .
.
设异面直线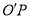 与
与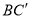 所成角为
所成角为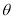 ,
,
则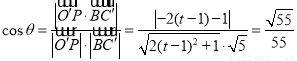 ,
,
化简得: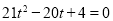 ,解得:
,解得: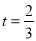 或
或 ,
,
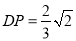 或
或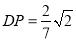 . 5分
. 5分
(2)∵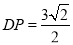 ,∴
,∴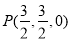 ,
,
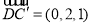 ,
,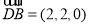 ,
,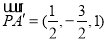 ,
,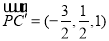 ,
,
设平面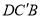 的一个法向量为
的一个法向量为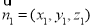 ,
,
∴ ,∴
,∴ ,即
,即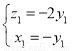 ,取
,取 ,
,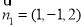 ,
,
设平面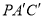 的一个法向量为
的一个法向量为 ,
,
∴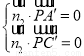 ,∴
,∴ ,即
,即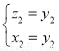 ,取
,取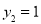 ,
, ,
,
设平面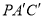 与平面
与平面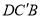 所成角为
所成角为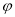 ,
,
∴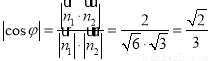 ,
,
∴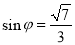 . 10分
. 10分
考点:利用空间向量求线线角及二面角
考点分析: 考点1:异面直线所成的角 考点2:线面所成的角 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 ,则
,则 则
则 _________________.
_________________. ,则
,则 =
=
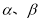 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)  ,则在平面
,则在平面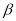 内,一定不存在与直线
内,一定不存在与直线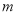 平行的直线.
平行的直线.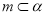 ,则在平面
,则在平面 的定义域为 .
的定义域为 .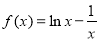 ,
,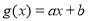 .
.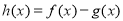 在
在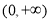 上单调递增,求实数
上单调递增,求实数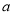 的取值范围;
的取值范围;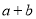 的最小值;
的最小值;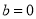 时,若
时,若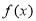 与
与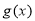 的图象有两个交点
的图象有两个交点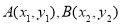 ,求证:
,求证: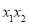
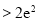 .
.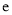 为
为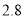 ,取
,取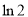 为
为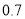 ,取
,取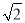 为
为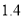 )
) 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 且
且 ,则
,则 中,
中,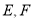 分别是
分别是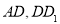 中点.
中点.
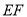 ∥平面
∥平面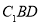 ;
;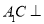 平面
平面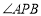 的平分线,
的平分线, 是下半圆的中点.求证:直线PC经过点
是下半圆的中点.求证:直线PC经过点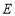 .
.