题目内容
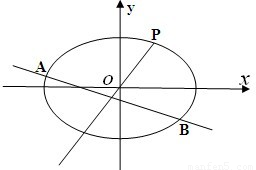
如图,在平面直坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,经过点
,经过点![]() ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆![]() 与直线
与直线![]() 有且只有一个交点。
有且只有一个交点。
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设不经过原点的直线![]() 与椭圆
与椭圆![]() 相交与A,B两点,第一象限内的点
相交与A,B两点,第一象限内的点![]() 在椭圆上,直线
在椭圆上,直线![]() 平分线段
平分线段![]() ,求:当
,求:当![]() 的面积取得最大值时直线
的面积取得最大值时直线![]() 的方程。
的方程。
 |
解:(Ⅰ)∵椭圆经过点![]() ,∴
,∴![]() 又
又![]() ,
,
∴![]() ,∴
,∴![]()
∴椭圆的方程为![]()
又∵椭圆![]() 与直线
与直线![]() 有且只有一个交点
有且只有一个交点
∴方程![]() 即
即![]() 有相等实根
有相等实根
∴![]() ∴
∴![]()
∴椭圆的方程为![]()
(Ⅱ)由(Ⅰ)知椭圆的方程为![]() 故
故![]()
设不经过原点的直线![]() 的方程
的方程![]() 交椭圆
交椭圆![]() 于
于![]()
由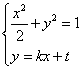 得
得![]()
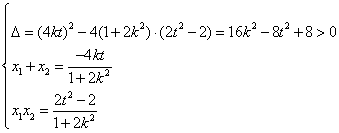
∴
![]()
…………
直线![]() 方程为
方程为![]() 且
且![]() 平分线段
平分线段![]()
∴![]() =
=![]()
![]() 解得
解得 ![]()
∴![]()
又∵点![]() 到直线
到直线![]() 的距离
的距离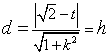
∴![]()
设![]()
由直线![]() 与椭圆
与椭圆![]() 相交于A,B两点可得
相交于A,B两点可得![]()
求导可得![]()
![]()
![]() ,此时
,此时![]() 取得最大值
取得最大值
此时直线![]() 的方程
的方程![]()

练习册系列答案
相关题目
 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆
 中,已知椭圆
中,已知椭圆 ,经过点
,经过点 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆 与直线
与直线 有且只有一个交点。
有且只有一个交点。
 与椭圆
与椭圆 在椭圆上,直线
在椭圆上,直线 平分线段
平分线段 ,求:当
,求:当 的面积取得最大值时直线
的面积取得最大值时直线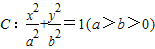 ,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线
,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线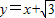 有且只有一个交点.
有且只有一个交点.