题目内容
设f(x)是定义在R上的周期函数,周期为T=4,对x∈R都有f(-x)=f(x),且当x∈[-2,0]时,f(x)=(
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实根,则a的取值范围是( )
| 1 |
| 2 |
| A、(1,2) | |||
| B、(2,+∞) | |||
C、(1,
| |||
D、(
|
考点:对数的运算性质,函数的周期性
专题:函数的性质及应用
分析:由已知得f(x+4)=
=f(x),函数f(x)是一个周期4的偶函数,函数y=f(x)与y=loga(x+2)在区间(-2,6]上有三个不同的交点,从而loga4<3,且loga8>3,由此能求出a的取值范围.
| 10 |
| f(x+2) |
解答:
 解:∵对于任意的x∈R,都有f(x)•f(x+2)=10,
解:∵对于任意的x∈R,都有f(x)•f(x+2)=10,
∴f(x+4)=
=f(x)
∴函数f(x)是一个周期函数,且T=4.
∵对x∈R都有f(-x)=f(x),
∴函数f(x)是定义在R上的偶函数,
∵当x∈[-2,0]时,f(x)=(
)x-1,
在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
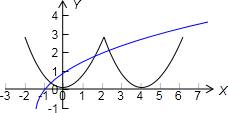
∴函数y=f(x)与y=loga(x+2)在区间(-2,6]上有三个不同的交点,
如右图所示:
又f(-2)=f(2)=3,
则有 loga4<3,且loga8>3,
解得:
<a<2,
故a的取值范围是(
,2).
故选:D.
 解:∵对于任意的x∈R,都有f(x)•f(x+2)=10,
解:∵对于任意的x∈R,都有f(x)•f(x+2)=10,∴f(x+4)=
| 10 |
| f(x+2) |
∴函数f(x)是一个周期函数,且T=4.
∵对x∈R都有f(-x)=f(x),
∴函数f(x)是定义在R上的偶函数,
∵当x∈[-2,0]时,f(x)=(
| 1 |
| 2 |
在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
∴函数y=f(x)与y=loga(x+2)在区间(-2,6]上有三个不同的交点,
如右图所示:
又f(-2)=f(2)=3,
则有 loga4<3,且loga8>3,
解得:
| 3 | 4 |
故a的取值范围是(
| 3 | 4 |
故选:D.
点评:本题考查实数的取值范围,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知p:2+2=5;q:3>2,则下列判断错误的是( )
| A、“p∨q”为真,“¬q”为假 |
| B、“p∧q”为假,“¬p”为真 |
| C、“p∧q”为假,“¬p”为假 |
| D、“p∨q”为真,“¬p”为真 |
函数f(x)=x2+bx(x≥0)是单调函数的充要条件是( )
| A、b≥0 | B、.b≤0 |
| C、b>0 | D、b<0 |
若数列{an}的前n项和为Sn=
an+
,则数列{an}的通项公式为( )
| 2 |
| 3 |
| 1 |
| 3 |
| A、an=-2n-1 |
| B、an=(-2)n-1 |
| C、an=(-2)n |
| D、an=-2n |
函数f(x)是定义在(-2,2)上的奇函数,当x∈(0,2)时,f(x)=2x-1,则f(log2
)的值为( )
| 1 |
| 3 |
| A、-2 | |||
B、-
| |||
| C、7 | |||
D、
|
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A、(一1,1) |
| B、(一1,+∞) |
| C、(一∞,一1) |
| D、(一∞,+∞) |
函数f(x)=lnx-
的零点所在的区间为( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |