题目内容
(本题满分12分)
底面边长为2的正三棱锥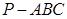 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ 的各边长及此三棱锥的体积
的各边长及此三棱锥的体积 .
.

底面边长为2的正三棱锥
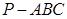 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ 的各边长及此三棱锥的体积
的各边长及此三棱锥的体积 .
.
边长为4,体积为 .
.
 .
.试题分析:由于展开图是
 ,
, 分别是所在边的中点,根据三角形的性质,
分别是所在边的中点,根据三角形的性质, 是正三角形,其边长为4,原三棱锥的侧棱也是2,要求棱锥的体积需要求出棱锥的高,由于是正棱锥,顶点
是正三角形,其边长为4,原三棱锥的侧棱也是2,要求棱锥的体积需要求出棱锥的高,由于是正棱锥,顶点 在底面上的射影是底面
在底面上的射影是底面 的中心,由相应的直角三角形可求得高,得到体积.
的中心,由相应的直角三角形可求得高,得到体积.试题解析:由题意
 中
中 ,
, ,
, ,所以
,所以 是
是 的中位线,因此
的中位线,因此 是正三角形,且边长为4.
是正三角形,且边长为4.
即
 ,三棱锥
,三棱锥 是边长为2的正四面体
是边长为2的正四面体∴如右图所示作图,设顶点
 在底面
在底面 内的投影为
内的投影为 ,连接
,连接 ,并延长交
,并延长交 于
于
∴
 为
为 中点,
中点, 为
为 的重心,
的重心, 底面
底面
∴
 ,
, ,
,
【考点】图象的翻折,几何体的体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为矩形,
为矩形, 平面
平面 ,
, ,作如图3折叠,折痕
,作如图3折叠,折痕 .其中点
.其中点 、
、 分别在线段
分别在线段 、
、 上,沿
上,沿 折叠后点
折叠后点 在线段
在线段 上的点记为
上的点记为 ,并且
,并且 .
.
 平面
平面 ;
; 的体积.
的体积. ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点. 平面
平面 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高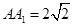 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点. 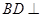 平面
平面 ;
; ∥平面
∥平面 ;
; 的体积.
的体积.

 ,且知
,且知 ,若仍用这个容器盛水,则最多可盛水的体积是原来的 .
,若仍用这个容器盛水,则最多可盛水的体积是原来的 .
 ,则原四边形的面积是多少?
,则原四边形的面积是多少?
 时,则该圆锥体的体积是 .
时,则该圆锥体的体积是 .