题目内容
如图K444所示,已知正方体ABCD A1B1C1D1的棱长为3,点E在AA1上,点F在CC1上,且AE=FC1=1.
(1)求证:E,B,F,D1四点共面;
(2)若点G在BC上,BG= ,点M在BB1上,GM⊥BF,垂足为H,求证:ME⊥平面BCC1B1.
,点M在BB1上,GM⊥BF,垂足为H,求证:ME⊥平面BCC1B1.

证明:(1)建立如图所示的空间直角坐标系,则B(0,0,0),E(3,0,1),F(0,3,2),D1(3,3,3),
则 =(3,0,1),
=(3,0,1), =(0,3,2),
=(0,3,2), =(3,3,3).
=(3,3,3).
因为 共面.
共面.
又它们有公共点B,所以E,B,F,D1四点共面.

 从而ME⊥BB1,ME⊥BC.
从而ME⊥BB1,ME⊥BC.
又BB1∩BC=B,所以ME⊥平面BCC1B1.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

 点M在OA上,且OM=2MA,N为BC的中点,则
点M在OA上,且OM=2MA,N为BC的中点,则 等于( )
等于( )
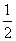 a-
a- 两两之间的夹角均为60°,且|
两两之间的夹角均为60°,且| |=1,
|=1, 则|
则| |等于( )
|等于( )
 B.
B.
 D.
D.
 取正数时,最小值为2 的是( )
取正数时,最小值为2 的是( )



 中已知AB=BC=1,
中已知AB=BC=1, ,
, ,D是
,D是 上的点,且
上的点,且


 的余弦值.
的余弦值.