Question

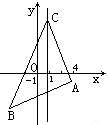
已知△ABC的一个顶点A（-1，-4），∠B、∠C的平分线所在直线的方程分别为l₁：y+1=0，l₂：x+y+1=0，求边BC所在直线的方程．

Answer 1

分析：由题意求A关于l₁：y+1=0，l₂：x+y+1=0的对称点坐标，它们都在BC直线上，从而得到答案．

解答：解：设点A（-1，-4）关于直线y+1=0的对称点为A′（x₁，y₁），则x₁=-1，y₁=2×（-1）-（-4）=2，即A′（-1，2）．
在直线BC上，再设点A（-1，-4）关于l₂：x+y+1=0的对称点为A″（x₂，y₂），则有

y2+4

x2+1

×（-1）=-1，

x2-1

2

+

y2-4

2

+1=0．
解得
x₂=3，
y₂=0，
即A″（3，0）也在直线BC上，由直线方程的两点式得

y-2

0-2

=

x+1

3+1

，即x+2y-3=0为边BC所在直线的方程．

点评：充分理解题意是解好题目的关键，本题就是充分利用了角的平分线方程，对称知识解答，是基础题．