题目内容
15.在自然界中存在着大量的周期函数,比如声波.若两个声波随时间的变化规律分别为:y1=3$\sqrt{2}$sin(100πt),y2=3cos(100πt+$\frac{π}{4}$),则这两个声波合成后(即y=y1+y2)的声波的振幅为( )| A. | $6\sqrt{2}$ | B. | $3+3\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 3 |
分析 利用和差化积公式即可得出.
解答 解:y=y1+y2=3$\sqrt{2}$sin(100πt)+3cos(100πt+$\frac{π}{4}$)
=3$\sqrt{2}$sin(100πt)+3×$\frac{\sqrt{2}}{2}$[cos(100πt)-sin(100πt)]
=3×$\frac{\sqrt{2}}{2}$[cos(100πt)+sin(100πt)]
=3sin(100πt+$\frac{π}{4}$),
则这两个声波合成后(即y=y1+y2)的声波的振幅为3.
故选:D.
点评 本题考查了和差化积公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10. 如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
 如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.函数f(x)=log3(2x-1)的零点是( )
| A. | 1 | B. | 2 | C. | (1,0) | D. | (2,0) |
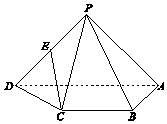 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1