题目内容
(本小题15分)
设数列{![]() }的前n项和为
}的前n项和为![]() ,并且满足
,并且满足![]() ,
,![]() (n∈N*).
(n∈N*).
(Ⅰ)求![]() ,
,![]() ,
,![]() ;
;
(Ⅱ)猜想{![]() }的通项公式,并用数学归纳法加以证明;
}的通项公式,并用数学归纳法加以证明;
(Ⅲ)设![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() ≤
≤![]() .
.
(本小题15分)
解:(Ⅰ)分别令![]() ,2,3,得
,2,3,得

∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
(Ⅱ)证法一:猜想:![]() ,由
,由 ![]() ①
①
可知,当![]() ≥2时,
≥2时,![]() ②
②
①-②,得 ![]() ,即
,即![]() .
.
1)当![]() 时,
时,![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
2)假设当![]() (
(![]() ≥2)时,
≥2)时,![]() .
.
那么当![]() 时,
时,
![]()
![]()
![]() ,
,
∵![]() ,
,![]() ≥2,∴
≥2,∴![]() ,
,
∴![]() .
.
这就是说,当![]() 时也成立,
时也成立,
∴![]() (
(![]() ≥2). 显然
≥2). 显然![]() 时,也适合.
时,也适合.
故对于n∈N*,均有![]()
(Ⅲ)要证![]() ≤
≤![]() ,
,
只要证![]() ≤
≤![]() ,
,
即![]()
![]() ≤
≤![]() ,
,
将![]() 代入,得
代入,得![]() ≤
≤![]() ,w.w.w.k.s.5 u.c.o.m
,w.w.w.k.s.5 u.c.o.m
即要证![]() ≤
≤![]() ,即
,即![]() ≤1.
≤1.
∵![]() ,
,![]() ,且
,且![]() ,∴
,∴![]() ≤
≤![]() ,
,
即![]() ≤
≤![]() ,故
,故![]() ≤1成立,所以原不等式成立.
≤1成立,所以原不等式成立.

练习册系列答案
相关题目
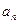 }的前n项和为
}的前n项和为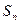 ,并且满足
,并且满足 ,
,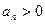 (n∈N*).
(n∈N*).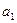 ,
,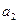 ,
,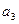 ;
; ,
,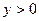 ,且
,且 ,证明:
,证明: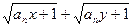 ≤
≤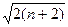 .
. 是虚数,
是虚数, 是实数,且
是实数,且 。
。 的值及
的值及 ,求证
,求证 为纯虚数;
为纯虚数; 的最小值.
的最小值.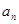 }的前n项和为
}的前n项和为 ,并且满足
,并且满足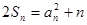 ,
,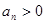 (n∈N*).
(n∈N*).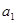 ,
,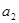 ,
,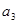 ;
;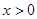 ,
, ,且
,且 ,证明:
,证明: ≤
≤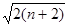 .
.