题目内容
(本小题15分)
设数列{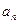 }的前n项和为
}的前n项和为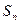 ,并且满足
,并且满足 ,
,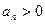 (n∈N*).
(n∈N*).
(Ⅰ)求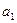 ,
,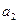 ,
,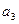 ;
;
(Ⅱ)猜想{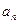 }的通项公式,并用数学归纳法加以证明;
}的通项公式,并用数学归纳法加以证明;
(Ⅲ)设 ,
,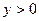 ,且
,且 ,证明:
,证明: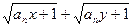 ≤
≤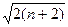 .
.
解:(Ⅰ)分别令 ,2,3,得
,2,3,得
∵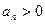 ,∴
,∴ ,
, ,
, .
.
(Ⅱ)证法一:猜想: ,由
,由  ①
①
可知, 当
当 ≥2时,
≥2时, ②
②
①-②,得  ,即
,即 .
.
1)当 时,
时, ,∵
,∵ ,∴
,∴ ;
;
2)假设当 (
( ≥2)时,
≥2)时, .
.
那么当 时,
时,

 ,
,
∵ ,
, ≥2,∴
≥2,∴ ,
,
∴ .
.
这就是说,当 时也成立,
时也成立, ∴
∴ (
( ≥2). 显然
≥2). 显然 时,也适合.
时,也适合.
故对于n∈N*,均有
(Ⅲ)要证 ≤
≤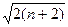 ,
,
只要证 ≤
≤ ,
,
即
 ≤
≤ ,
,
将 代入,得
代入,得 ≤
≤ ,
,
即要证 ≤
≤
 ,即
,即 ≤1.
≤1.
∵ ,
,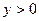 ,且
,且 ,∴
,∴ ≤
≤ ,
,
即 ≤
≤ ,故
,故 ≤1成立,所以原不等式成立.
≤1成立,所以原不等式成立.
解析

(本小题满分12分)
某班全部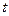 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是 按上述分组方式得到的频率分布表。
按上述分组方式得到的频率分布表。
| 分 组 | 频数 | 频率 |
| [13,14) |  | 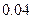 |
| [14,15) | 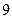 | 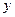 |
| [15,16) | 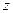 |  |
| [16,17) | 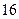 | 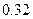 |
| [17,18] | 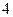 | 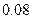 |
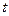 及上表中的
及上表中的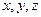 的值;
的值;(2)设m,n是从第一组或第五组中任意抽取的两名学生的
 百米测试成绩,求事件“
百米测试成绩,求事件“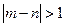 ”的
”的 概率.
概率. (本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
|
尺寸 |
|
|
|
|
|
|
|
甲机床零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
|
乙机床零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元. 若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: .
.
参考数据:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
(本小题满分12分)
某班全部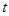 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
|
分 组 |
频数 |
频率 |
|
[13,14) |
|
|
|
[14,15) |
|
|
|
[15,16) |
|
|
|
[16,17) |
|
|
|
[17,18] |
|
|
(1)求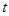 及上表中的
及上表中的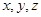 的值;
的值;
(2)设m,n是从第一组或第五组中任意抽取的两名学生的百米测试成绩,求事件“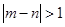 ”的概率.
”的概率.
(本小题满分12分)
某班全部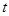 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
|
分 组 |
频数 |
频率 |
|
[13,14) |
|
|
|
[14,15) |
|
|
|
[15,16) |
|
|
|
[16,17) |
|
|
|
[17,18] |
|
|
(1)求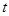 及上表中的
及上表中的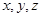 的值;
的值;
(2)设m,n是从第一组或第五组中任意抽取的两名学生的百米测试成绩,求事件“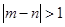 ”的概率.
”的概率.




























