题目内容
已知正实数a，b满足a+b=1，则M=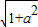
+
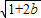的整数部分是（ ）A．1或2
B．2
C．2或3
D．3
【答案】分析：由题意可得a∈（0，1），b∈（0，1），由不等式的放缩法可得：M＞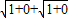
=2；M＜
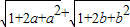=3，进而可得答案．
解答：解：由题意可得a∈（0，1），b∈（0，1），
由不等式的放缩法可得：M＞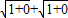
=2；
M＜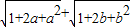
=
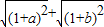
=|1+a|+|1+b|=1+a+1+b=3，
故2＜M＜3，即M的整数部分为：2
故选B
点评：本题考查不等式的放缩法，适当的放缩是解决问题的关键，属中档题．
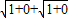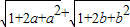=2；M＜=3，进而可得答案．解答：解：由题意可得a∈（0，1），b∈（0，1），
由不等式的放缩法可得：M＞
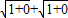=2；M＜
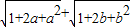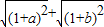
==|1+a|+|1+b|=1+a+1+b=3，
故2＜M＜3，即M的整数部分为：2
故选B
点评：本题考查不等式的放缩法，适当的放缩是解决问题的关键，属中档题．
练习册系列答案
相关题目
已知正实数a、b满足a+b=1，则
的最大值为（ ）
| ab |
| 4a+9b |
A、
| ||
B、
| ||
C、
| ||
D、
|