题目内容
6.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+3$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的正弦值为$\frac{\sqrt{15}}{4}$.分析 由向量垂直的条件可得($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+3$\overrightarrow{b}$)=0,化简可得$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$,再由向量的夹角公式可得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>,再由同角的平方关系,可得夹角的正弦值.
解答 解:|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|=2,即为|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,
($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$+3$\overrightarrow{b}$),
可得($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+3$\overrightarrow{b}$)=0,
即有$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$-3$\overrightarrow{b}$2=0,
即4+2$\overrightarrow{a}$•$\overrightarrow{b}$-3=0,
即有$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$,
即cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-\frac{1}{2}}{2×1}$=-$\frac{1}{4}$,
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,
即有sin<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\sqrt{1-(-\frac{1}{4})^{2}}$=$\frac{\sqrt{15}}{4}$.
故答案为:$\frac{\sqrt{15}}{4}$.
点评 本题考查向量的数量积的定义和性质,考查向量夹角的正弦,考查运算能力,属于中档题.

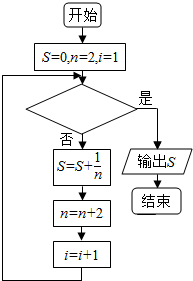 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i≥49? | B. | i≥50? | C. | i≥51? | D. | i≥100? |