题目内容
6.若数列{an}的通项公式是an=(-1)•(3n-2),求数列{an}的前n项和Sn.分析 由已知可得,数列{an}是以-1为首项,以-3为公差的等差数列,代入等差数列的前n项和公式求得答案.
解答 解:由an=(-1)•(3n-2),得a1=-1,
且an+1-an=(-1)•(3n+1)-(-1)•(3n-2)
=(-1)•(3n+1-3n+2)=-3.
∴数列{an}是以-1为首项,以-3为公差的等差数列,
则${S}_{n}=-n+\frac{n(n-1)(-3)}{2}=\frac{-3{n}^{2}+n}{2}$.
点评 本题考查等差关系的确定,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
17.已知平行于x轴的直线分别交曲线y=e2x+1与y=$\sqrt{2x-1}$于A,B两点,则|AB|的最小值为( )
| A. | $\frac{5+ln2}{4}$ | B. | $\frac{5-ln2}{4}$ | C. | $\frac{3+ln2}{4}$ | D. | $\frac{3-ln2}{4}$ |
18.设p:?x0∈R,-x${\;}_{0}^{2}$+2x0-m>0,q:函数f(x)=$\frac{1}{3}$x3-2x2+4mx+1在R内使增函数,则¬p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知集合A={x|y=1n(1-x2)},B={y|y=1n(1-x2)},则CR(A∩B)=( )
| A. | (-∞,-1)∪(0,+∞) | B. | (-∞,-1]∪[0,+∞) | C. | (-1,0) | D. | [-1,0] |
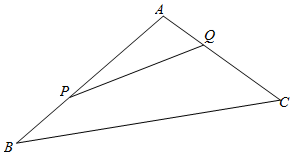 如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.
如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米.