题目内容
 如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).
如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).(Ⅰ)求证:BD⊥平面AOC′;
(Ⅱ)若AC′=2
| 5 |
| 11 |
| 21 |
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)利用直线与平面垂直的判定定理直接证明:BD⊥平面AOC′;
(Ⅱ)判断∠BED为二面角B-AC′-D的平面角,通过AC′=2
,二角面B-AC′-D的余弦值为
,直接求出BD的长.
(Ⅱ)判断∠BED为二面角B-AC′-D的平面角,通过AC′=2
| 5 |
| 11 |
| 21 |
解答:
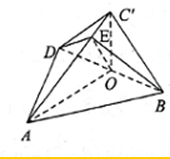 (Ⅰ)证明:在图中,因为AB=AD,BC=CD,所以在直线AC为线段BD的中垂线,所以,BD⊥AO,BD⊥CO,则在图2中有BD⊥AO,BD⊥C′O,而AO∩C′O=O,所以BD⊥平面AOC′.
(Ⅰ)证明:在图中,因为AB=AD,BC=CD,所以在直线AC为线段BD的中垂线,所以,BD⊥AO,BD⊥CO,则在图2中有BD⊥AO,BD⊥C′O,而AO∩C′O=O,所以BD⊥平面AOC′.
(Ⅱ)解:由条件可知,AO=4,C′O=2,AC′=2
,即AC′2=AO2+C′O2,
所以AO⊥C′O,所以AO⊥C′O,
过O作OE⊥AC′,垂足为E,连结BE,DE,由(Ⅰ)可知BD⊥平面AOC′,
所以BE⊥AC′,DE⊥AC′,所以∠BED为二面角B-AC′-D的平面角,
在Rt△AOC′中,由条件可得OE=
,设BD=2a,则BO=DO=a,
所以BE=DE=
=
,
在△BDE中,由余弦定理得BD2=BE2+DE2-2BE•DEcos∠BED,
即:4a2=2(a2+
)-2(a2+
)•
,
解得a=1,所以BD=2.
 (Ⅰ)证明:在图中,因为AB=AD,BC=CD,所以在直线AC为线段BD的中垂线,所以,BD⊥AO,BD⊥CO,则在图2中有BD⊥AO,BD⊥C′O,而AO∩C′O=O,所以BD⊥平面AOC′.
(Ⅰ)证明:在图中,因为AB=AD,BC=CD,所以在直线AC为线段BD的中垂线,所以,BD⊥AO,BD⊥CO,则在图2中有BD⊥AO,BD⊥C′O,而AO∩C′O=O,所以BD⊥平面AOC′.(Ⅱ)解:由条件可知,AO=4,C′O=2,AC′=2
| 5 |
所以AO⊥C′O,所以AO⊥C′O,
过O作OE⊥AC′,垂足为E,连结BE,DE,由(Ⅰ)可知BD⊥平面AOC′,
所以BE⊥AC′,DE⊥AC′,所以∠BED为二面角B-AC′-D的平面角,
在Rt△AOC′中,由条件可得OE=
| 4 | ||
|
所以BE=DE=
a2+(
|
a2+
|
在△BDE中,由余弦定理得BD2=BE2+DE2-2BE•DEcos∠BED,
即:4a2=2(a2+
| 16 |
| 5 |
| 16 |
| 5 |
| 11 |
| 21 |
解得a=1,所以BD=2.
点评:本题考查直线与平面垂直的判定定理,二面角的平面角的求法与应用,考查空间几何体的应用.

练习册系列答案
相关题目
等比数列{an}中,若a1•a2=4,a5•a6=16,则a3•a4=( )
| A、8 | B、10 | C、12 | D、14 |
已知集合A={x∈R|(x+1)(x-3)>0},B={x∈R|3x+2>0},则A∩B=( )
| A、(3,+∞) | ||
B、(-
| ||
C、(-1,-
| ||
| D、(-∞,-1) |