Question

11．求证：直角坐标平面上的格点凸七边形（每个顶点均为格点--纵、横坐标均为整数的点）的内部最少包含四个格点．

Answer 1

分析 不妨设格点凸七边形ABCDEFG的各边的内部都没有格点，再由五边形AMEFG可确定另一个格点，从而推导出结论．

解答 解：首先，不妨设格点凸七边形ABCDEFG的各边的内部都没有格点（否则，如FG的内部有一个格点H，
则用七边形ABCDEFH）代替原来的七边形，由于格点个数有限，故这种过程一定会在某一步终止）．
其次，任何五个格点或五个顶点的坐标按奇偶性分类，至多有四类：（奇，奇）（奇，偶）（偶，偶）（偶，奇）．
故必有五个顶点中的某两个点属于一类，这两点的中点M也是格点，且点M在凸七边形的内部．
考虑A、B、C、D、E这五个格点，其中某两点的中点M也是格点，且点M在凸七边形ABCDEFG的内部．
同理，由格点五边形AMEFG可确定另一个格点N，也在七边形ABCDEFG的内部．
直线MN将平面分为两部分，其中必有某一侧至少含有格点凸七边形的三个顶点．
不妨设A、B、G在MN的同一侧，则由凸五边形ABMNG知，七边形ABCDEFG的内部还有第三个格点P．
（1）若MN的另一侧也含有七边形ABCDEFG的三个顶点，同理可得第四个格点Q，
（2）若MN的另一侧至多含两个顶点D和E，则C、F在直线MN上或与A、B、G在MN的同一侧，
这时又有两种情况：
（i）若点P不在△ABM内，则A、B、C、M、P组成凸五边形，故可得第四个格点Q，
（ii）若点P在△ABM内（或边上），则A、P、N、F、G组成凸五边形，故可得第四个格点Q．
另一方面，凸七边形的内部包含四个格点的图象如下，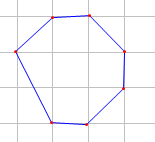
．

点评 本题考查了归纳推理的应用，属于难题．