题目内容
已知直线l经过直线2x+y-5=0与x-2y=0的交点.
(1)若点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值,并求此时l的方程.
(1)若点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值,并求此时l的方程.
分析:(1)当斜率存在时,设出直线方程y-1=k(x-2),先联立两条直线的解析式求出两条直线的交点坐标代入直线方程即可求出k;当斜率不存在时,验证是否符合题.从而得出答案.
(2)先由题意可知点A(5,0)到直线l的距离最大时即为P(2,1)与A(5,0)确定的直线与直线l垂直,根据两直线垂直时斜率乘积为-1得到直线l的斜率,即可得到直线l的方程.
(2)先由题意可知点A(5,0)到直线l的距离最大时即为P(2,1)与A(5,0)确定的直线与直线l垂直,根据两直线垂直时斜率乘积为-1得到直线l的斜率,即可得到直线l的方程.
解答: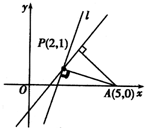 解:(1)联立
解:(1)联立
得交点P (2,1).设l的方程为
y-1=k(x-2)(k存在),即 kx-y-2k+1=0
∵
=3,得(3k+1)2=9(k2+1),
即k=
,∴l的方程为4x-3y-5=0.
当k不存在时,直线l:x=2,此时点A(5,0)到l的距离也为3.
∴直线l的方程为 x=2或4x-3y-5=0…(6分)
(2)由
解得交点P(2,1),
如图,过P任作一直线l,设d为定点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).
∴dmax=|PA|=
,kPA=-
,又kl×kPA=-1,∴kl=3
∴直线l的方程y-1=3(x-2)即:3x-y-5=0.…(12分)
 解:(1)联立
解:(1)联立
|
y-1=k(x-2)(k存在),即 kx-y-2k+1=0
∵
| |5k-2k+1| | ||
|
即k=
| 4 |
| 3 |
当k不存在时,直线l:x=2,此时点A(5,0)到l的距离也为3.
∴直线l的方程为 x=2或4x-3y-5=0…(6分)
(2)由
|
如图,过P任作一直线l,设d为定点A到l的距离,则d≤|PA|(当l⊥PA时等号成立).
∴dmax=|PA|=
| 10 |
| 1 |
| 3 |
∴直线l的方程y-1=3(x-2)即:3x-y-5=0.…(12分)
点评:考查学生会根据两直线方程求出交点坐标,会根据斜率和一点坐标求直线的一般式方程.要求学生要会灵活运用点到直线的距离公式求值,同时会利用两直线垂直时斜率乘积为-1解决数学问题.

练习册系列答案
相关题目