题目内容
已知甲乙进行游戏,甲胜的概率为0.8,乙胜的概率为0.2,若共进行10场游戏,问甲至少赢2场的概率是多少?
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:首先设事件A=甲赢1场或一场不赢,求出P(A),然后用1减去P(A),即可求出甲至少赢2场的概率是多少,据此解答即可.
解答:
解:设事件A=甲赢1场或一场不赢,
则P(A)=
0.800.210
0.810.29
=0.0000001024+0.000004096
=0.0000041984
所以甲至少赢2场的概率是:
1-P(A)=1-0.0000041984=0.9999958016.
答:甲至少赢2场的概率是0.9999958016.
则P(A)=
| C | 0 10 |
| +C | 1 10 |
=0.0000001024+0.000004096
=0.0000041984
所以甲至少赢2场的概率是:
1-P(A)=1-0.0000041984=0.9999958016.
答:甲至少赢2场的概率是0.9999958016.
点评:本题主要考查了相互独立事件概率乘法公式的运用,考查了互斥事件的概率加法公式的运用,属于中档题,解答此题的关键是求出甲至少赢2场的对立事件的概率是多少.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知α+β=3π,下列等式恒成立的是( )
| A、sinα=sinβ |
| B、cosα=cosβ |
| C、sinα=cosβ |
| D、tanα=tanβ |
函数y=xlnx的减区间为( )
A、(-∞,
| ||
B、(
| ||
C、(0,
| ||
| D、(0,+∞) |
若lg2=a,lg3=b,则log26=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}满足a7+a8+a3=15,函数fn(x)=sin(
x+
),那么f5(a6)的值为( )
| π |
| n |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
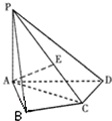 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.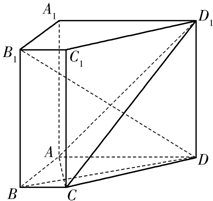 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.