题目内容
1.六名同学A、B、C、D、E、F举行象棋比赛,采取单循环赛制,即参加比赛的每两个人之间仅赛一局.第一天,A、B各参加了3局比赛,C、D各参加了4局比赛,E参加了2局比赛,且A与C没有比赛过,B与D也没有比赛过.那么F在第一天参加的比赛局数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 从A、B各参加了3局比赛,C、D各参加了4局比赛,E参加了2局比赛,且A与C没有比赛过,B与D也没有比赛过这个已知条件入手,进而可一步一步推得每个人分别与那几个人下了几局,最后即可得出F最终下了几局.
解答 解:由于A、B各参加了3局比赛,C、D各参加了4局比赛,E参加了2局比赛,且A与C没有比赛过,B与D也没有比赛过,
所以与D赛过的是A、C、E、F四人;
与C赛过的是B、D、E、F四人;
又因为E只赛了两局,A与B各赛了3局,
所以与A赛过的是D、B、F;
而与B赛过的是A、C、F;
所以F共赛了4局.
故选D.
点评 本题主要考查了推理与论证的问题,能够通过已知条件找出突破口,从而通过推理得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在△ABC中,a,b,c分别是A,B,C的对边,$a=2\sqrt{3},b=2\sqrt{2}$,且1+2cos(B+C)=0,则BC边上的高等于( )
| A. | $2({\sqrt{3}+1})$ | B. | $2({\sqrt{3}-1})$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
9.在△ABC中,角A,B,C所对的边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则sinAcosBsinC=( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{\sqrt{3}}{8}$ |
16.已知集合A={-1,1,2,3},B={x|x≥2},那么A∩B等于( )
| A. | {3} | B. | {2,3} | C. | {-1,2,3} | D. | {-1,1,2,3} |
13.实数x,y满足$\left\{\begin{array}{l}x≤3\\ x+y≥0\\ x-y+6≥0.\end{array}\right.$若z=ax+y的最大值为3a+9,最小值为3a-3,则a的取值范围是( )
| A. | [-1,0] | B. | [0,1] | C. | [-1,1] | D. | (-∞,-1]∪[1,+∞) |
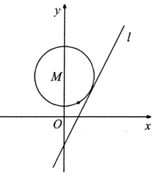 已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).
已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1). 如图,四棱锥P-ABCD的底面为矩形,PA是四棱锥的高,AP=AB=2,F是PB的中点,E是BC上的动点.
如图,四棱锥P-ABCD的底面为矩形,PA是四棱锥的高,AP=AB=2,F是PB的中点,E是BC上的动点.