题目内容
当正整数的集合A满足:“若x∈A,则12-x∈A”时,(1)试写出只有一个元素的集合;
(2)试写出只有两个元素的集合;
(3)这样的集合至多有多少个元素?
解:(1)∵集合A中只有一个元素,∴x=12-x,x=6,即A={6}.
(2)∵集合A中只有两个元素,且满足当x∈A时,12-x∈A,
∴这两个元素之和为12.又集合A为正整数集,
∴集合A可以为{1,11},{2,10},{3,9},{4,8},{5,7}.
(3)结合(1)(2)知集合A中的元素最多有11个,此时A={1,2,3,4,5,6,7,8,9,10,11}.

练习册系列答案
相关题目
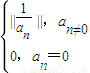 其中n=1,2,3,…
其中n=1,2,3,…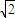 ,求数列{an};
,求数列{an};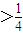 时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A.
时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A.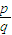 (p 是整数,q是正整数,p、q互质),问对于大于q的任意正整数n,是否都有an=0成立,并证明你的结论.
(p 是整数,q是正整数,p、q互质),问对于大于q的任意正整数n,是否都有an=0成立,并证明你的结论.